Attention Mechanism
CodeT5를 비롯한 거의 모든 transformer 기반의 모델들이 Attention Mechanism에 기반을 두고 있기에, Attention Machenism이 무엇인지, 기존의 hidden state만을 사용하는 모델들과는 어떤 부분에서 차이가 나는지를 공부해 보았다.
이번 정리는 아래 링크를 참고했다.
Context
- Attention Mechanism 정의
- Attention Mechanism 구현
- Attention score 계산
- Attention Distribution 계산
- Attention Value 계산
- Concatenate Vector 계산
- Hidden State Update
1. Attention Mechanism
기존의 RNN 기반의 Seq2Seq 모델에서 인코더와 디코더를 연결해주는 Context Vector가 존재했다.
이 Context Vector의 경우, 하나의 고정된 크기의 벡터로 정보를 압축하고, 이를 활용하여 정답값을 예측하는 과정이기에, 정보 손실이 발생하며 추가적으로, RNN의 고질적인 문제인 기울기 소실 문제(Vanishing Gradient Problem)이 발생한다.
결론적으로 Seq2Seq 모델은 1.정보 손실 2. 기울기 소실 등등의 문제로 인해서 입력의 크기가 커질수록 RNN의 성능이 떨어지는 것으로 확인되었다.
이런 문제를 해결하기 위해서 인코더의 입력 문장 전체를 다시 한 번 참고하는 방식을 사용하여 해결하게 되는데, 이를 Attention이라고 부른다. 다만, 이는 전체 문장을 동일한 비율로 참고하는 것이 아니라, 특정 입력에 대해 더 높은 가중치를 주며 활용한다.
2. Attention Mechanism 구현
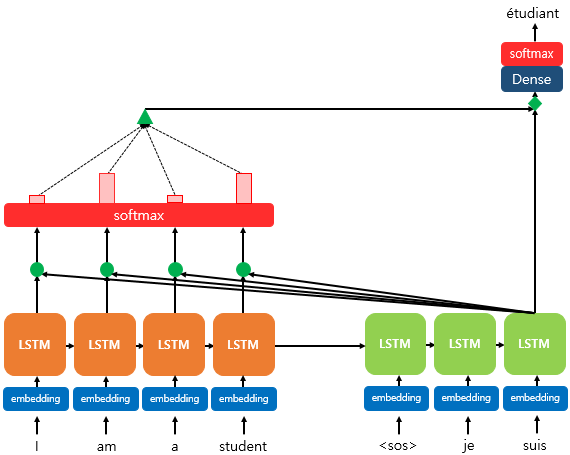
위의 그림은 Seq2Seq + Attention 기법이 적용된 모델에서 각 단어를 예측하는 과정을 보여준다. 여기서 예측하는 값은 세번째 LSTM Cell에서의 출력 단어다. 세번째 Cell에서, LSTM의 Hidden state를 활용하여, 현재 값과 input 값들이 얼마나 관련이 있는지를 계산하고, 이 정보와 Hidden state를 활용하여 출력값을 결정하는 방식으로 사용된다.
2.1 Attention Score 계산
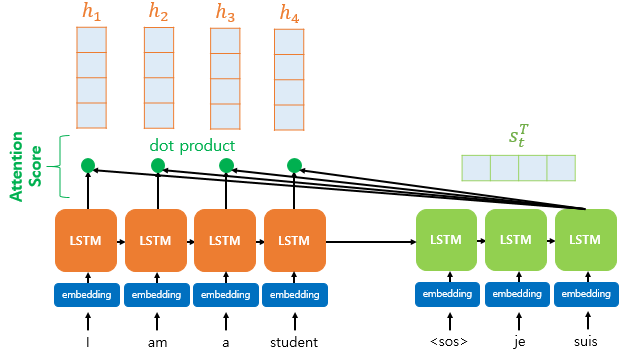
Seq2Seq + Attention 구조를 가진 RNN에 대해서 Attention Score를 계산하려면, 각 Decoder Cell에 입력드로 들어가는 hidden state를 활용하여 Attention Score를 계산해주어야 한다.
Decoder의 hidden state 길이와 Encoder의 hidden state 길이가 동일하다고 가정한다면, 예측하려는 Decoder Cell의 hidden state (\(s_t\))와 Encoder Cell의 hidden state(\(h_1, h_2, ..., h_n\))의 구조가 동일할 것이다.
따라서, \(s_t\)와 \(h_1, h_2, ..., h_n\)시퀀스의 dot production을 진행할 수 있게 되기에, 해당 연산을 진행한 값을 \(e^t\)로 정의할 수 있고, 해당 식을 아래와 같이 표현할 수 있다.
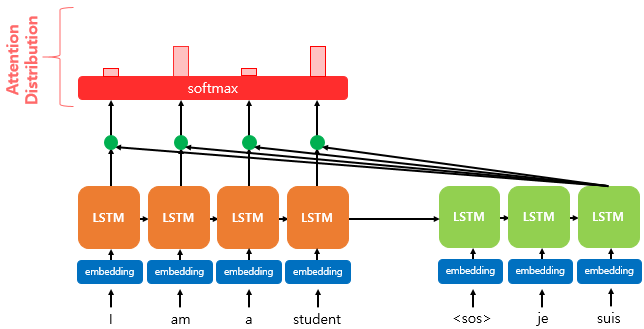
2.2 Attention Distribution 계산
앞에서 구한 \(e^t\) 벡터는 각 encoder의 hidden state와 예측하려는 Decoder cell과의 관계를 나타내는 Vector로 생각할 수 있다. 이제 해당 벡터에 SoftMax 함수를 적용하여 분포 형태로 만들어주는데, 이를 Attention Distribution이라고 부른다.
\[a^t = softmax(e^t)\]SoftMax 함수를 적용한 분포는 결국, Decoder의 특정 Cell에서 각 Encoder Input이 얼마나 많은 기여도를 가지는지를 의미하므로, 이를 바탕으로 Attention Value를 계산하는 데에 활용할 수 있다.
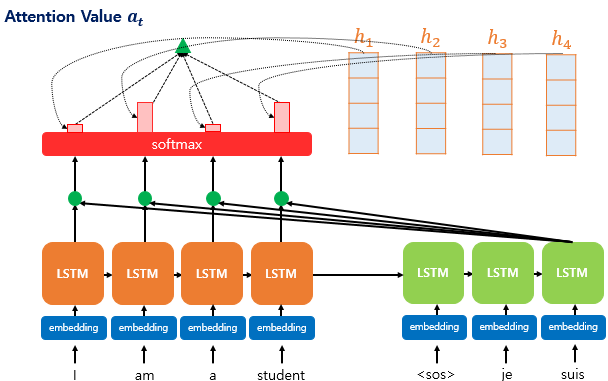
2.3 Attention Value 계산
앞서 계산한 Attention Distribution을 바탕으로 Attention Value를 계산할 수 있다. 앞서 계산한 가중치를 각 Encoder의 hidden state에 scalar 곱을 진행하여 state들을 전부 더해준다면, Attention Value를 구할 수 있고, 이를 Context Vector라고도 부른다.
이를 수식으로 표한하면 아래와 같다.
\[a_t = \sum_{i=1}^{N} a^t_ih_i\]해당 연산을 통해서 구해진 Context Vector는 인코더의 문맥을 포함하고 있다고 볼 수 있고, 입력의 길이가 길어지면, 정보의 소실이 발생하는 문제를 어느정도 해결할 수 있다.
2.4 Concatenate Vector 계산
위의 Attention Value를 구하고, Attention Distribution을 구하고 최종적으로 생성한 Attention Value \(a_t\)는 결국 기존의 s_t와 결합되어 하나의 벡터로 만들어주어야 하고, 이를 통해서 Attention Mechanism이 정상적으로 동작할 수 있게 되는 것이다.
Encoder의 hidden state와 Deccoder의 hidden state를 동일한 크기로 가정했을 때, Attention Value의 경우도 동일한 크기를 가질 것이기에, Concatenate된 Vector는 기존 hidden state의 2배의 길이를 가지게 된다.
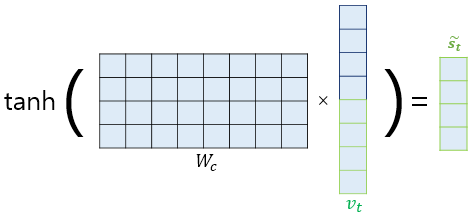
2.5 Hidden state Update
앞서 계산한 Concatenate Vector를 생각해보자. Hidden state 대비 2배의 길이를 가진 이 벡터를 hidden state로 활용하기 위해서, 전처리에 해당하는 과정을 진행해주어야 한다. 간단히 말해 벡터의 사이즈를 원하는 크기에 맞게 조정해주어야 한다는 것이다.
이 과정에서, 여러가지 방법이 존재하겠지만, FC Layer 형태의 Linear Regression과 Tanh의 activation Function을 사용할 수 있다. 해당 과정을 거쳐, hidden state를 updating할 수 있다.
이때, 사용하는 가중치 \(W_c, b_c\)는 학습이 가능한 것들이다.
해당 과정을 거쳐 업데이트한 값들을 이용하여 결과값 예측에 사용할 수 있다.
정리
다양한 종류의 Attention 기법이 많이 존재하지만, 다른 Attention 기법들은 Attention Score을 구하는 과정에 있어서 주로 차이가 발생한다.