Beam_Search 정리

BIFI 논문을 읽으면서 Beam Search에 관한 내용이 있었기에 이에 관한 정리를 하고자 한다.

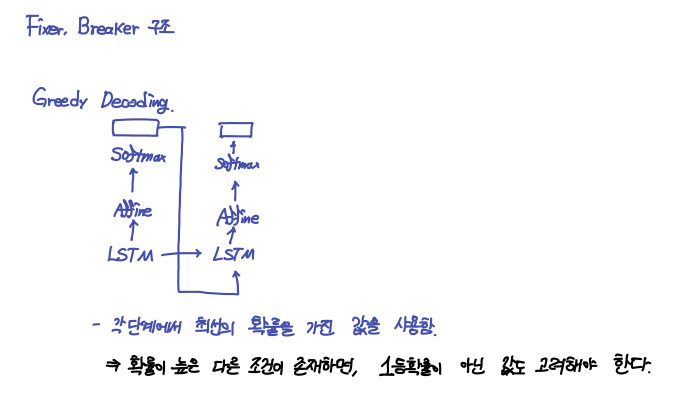
Greedy Decoding

Greedy Decoding 방식은 Seq2Seq 모델에서 Decoder에서 현재 시점에서 가장 높은 확률을 가진 후보를 선택하는 방식을 사용하는 것이다.
Greedy Decoding 방식은 복잡도 관점에서는 좋은 방식이지만, 최종 정확도에서는 낮은 모습을 보일 수 있다.
아래는 Seq2Seq 모델을 간단히 나타낸 모델이다.

특정 시점에서 후보군들의 확률을 계산하고, 2등, 3등의 확률은 전혀 신경쓰지 않고, 1등만 신경쓰므로, 만약 1등과 2등의 차이가 작고, 2등이 맞는 답이라면, 이전 예측이 중요한 Decoder의 역할은 제대로 수행되지 못할 것이다.

Beam Search Decoding

Beam Search 방식은 Greedy Decoding 방식을 개선하기 위해 사용된 Search 방식이다.
Beam Search 방식은 간단히 말해 누적 확률을 계산하고, 가장 누적 확률이 높은 후보를 선택하는 방식이다.
모든 누적 확률을 계산하는 것이 불가능하기에, k개의 빔을 설정하고 Beam Search에 활용한다.
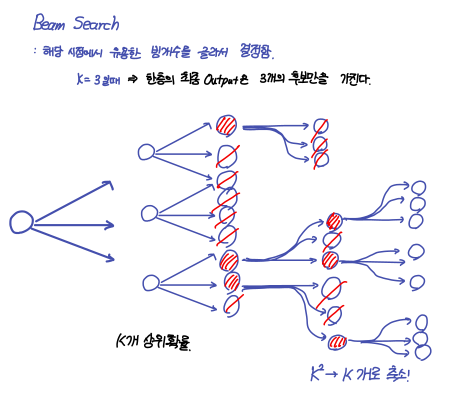
아래는 Beam Search를 그림으로 나타낸 것이다.

Beam Search는 아래와 같은 방식으로 진행된다.
1. start of sequence로부터 상위 k개 후보를 고른다.
2. k개의 후보들의 하위 후보 각각을 k개만큼 고른다. 총, k^2개의 후보가 골라진다.
3. 2.에서 고른 후보들 중에서 누적 확률 상위 k개 만큼을 고른다.
4. 2,3을 반복하면서 sign이 나오면 해당 후보를 candidate(후보군)으로 유지하고 개수만큼 추가 후보를 뽑는다.
  
  이때, 상위 누적 확률에 따라서 추가 후보를 뽑는 방식이다.
5. 이를 계속해서 반복하다가 k개의 candidate를 뽑는 순간 종료한다.
6. 종료 이후 누적 확률이 가장 큰 candidate를 선택한다.

Beam Search 방식에서의 누적 확률 계산

위에서 설명한 Beam Search 방식을 사용할 때, 누적 확률을 사용한다.

확률이란 0 ~ 1 사이의 값을 가지기에, 이를 무턱대고 곱하는 단순한 연산을 사용한다면, 짧은 대답에 가중치를 주는 것과 동일하다.

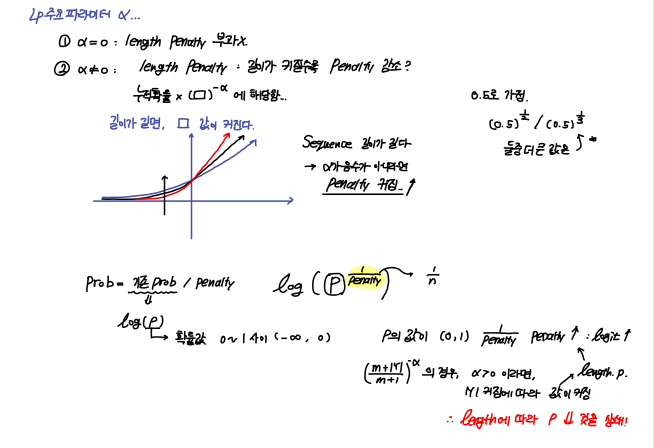
이런 문제를 해결하기 위해, Beam Search 방식에서의 누적 확률 계산은 Length Penalty를 이용한다.

Length penalty를 사용하여 길이가 짧은 경우에 더 큰 값, 길이가 긴 sequence에 더 작은 값을 부여하여 기존의 확률곱/Length_penalty 방식으로 사용되는 방식에서 길이로 인한 penalty를 조금이나마 해소할 수 있게 된다.

Length Penalty 공식을 사용한다면, 길이가 길어질수록 LP의 값이 커지는 것을 확인할 수 있고, 이를 활용하면, 지수함수의 특성 상 짧은 길이가 긴 길이보다 더 작은 밑 값을 가지는 것을 확인할 수 있고, hyperparameter에 해당하는 알파값이 0 이하가 아니라면, 패널티에 의해서 길이가 짧은 candidate의 확률을 줄이고, 길이가 긴 candidate의 확률은 높여 누적확률을 사용할 수 있게 된다.

Beam_Search 정리