CS231n - Lecture 2

#2 - Image Classification

Image Classification
Difficulties of Image Classification
Image Classification with Machine Learning
- Nearest Neighbor Algorithm
  - Introduction
  - Full Code (Python)
  - Problem
- K-Nearest Neighbor Algorithm(KNN)
  - Supplement of KNN
Distance Metric
Hyperparameter
- Introduction
- Controlling Data Set for Hyperparameter
Limitations of KNN in terms of Image Classification
Linear Classification
- Parametric Approach
- Parametric Approach in Linear Classification
- Meaning of M&X&B matrix
- Pros and Cons of Parametric Approach in terms of Image Classification
Summary

Image Classification

**Image Classification **(이미지 분류) - Computer Vision에 있어서 핵심적인 과제

이 Image Classification 문제를 어떻게 다룰 것인지가 이 수업의 핵심이다.

간략하게 이 과정을 정리하면 아래와 같다.

	1.  시스템이 분류의 대상이 되는 이미지인 Input Image를 입력받는다.
	2.  시스템은 미리 입력된 Category나 Label Set를 이용하여 Input Image에 Categories나 Labels들 중 하나를 할당해준다.

Difficulties of Image Classification

인간의 눈에는 이미지를 인식하는 과정이 쉽지만, 기계가 이미지를 인식하는 데에는 큰 어려움이 있다.

우리에게는 익숙한 고양이처럼 보이는 사진도, 기계의 입장에서는 수천개의 행과 열로 이루어진 숫자들로 이루어져 있기에 고양이인지 파악하기는 쉽지 않다. 이를 우리는 Semantic Gap (의미론적 차이) 라구 한다.

우리가 고양이라고 의미부여한 것이 Semantic Idea이고, 이는 기계가 인식하는 Pixel Value와 상당히 많은 차이가 있다. 같은 고양이라고 할 지라도 카메라의 방향이 조금이라도 달라지면 Pixel Value는 달라지지만, Semantic Idea는 그대로이다. 따라서 기계의 알고리즘은 이런 차이에 대해서 초연해야 하기에, Semantic Gap 문제가 해결하기 어렵다.

해결해야 할 문제는 다음과 같다.

Illumination - 광원의 위치에 따라서 Pixel들의 값은 완전히 달라진다.
Deformation - 사물의 모양이 달라져도 동일한 Label로 분류해야 한다.
Occlusion - 사물의 전체 모양이 보이지 않고 일부분만 보여도 동일한 Label로 분류할 수 있어야 한다.
Background Clutter - 사물의 이미지의 배경과 비슷한 경우에도 사물을 인식하여 분류할 수 잇어야한다.
Intraclass Variation - 동일한 사물이라고 할지라도 각기 다른 생김새나 크기를 가지지만, 이를 인식하고 사물을 분류할 수 있어야 한다.

인간의 뇌는 이를 가능하게 특별히 진화해왔지만, 기계의 입장에선 굉장히 힘든 문제들이다.

Image Classification with Machine Learning

RSA 암호화 알고리즘, 숫자 정렬 알고리즘의 경우에는 순차적인 High-end 방식으로 코딩이 가능했지만, 이미지 인식 알고리즘의 경우는 명확하고 순차적인 High-ended coding이 힘들다.

사실 몇가지 Explicit Attempt들이 있었다. 모서리, 꼭짓점, 경계선 등의 정보를 이용하여 어떤 사물은 몇개의 경계선이 모여 꼭짓점을 이룬다 등등의 규칙을 만들어 사물을 인식하려는 시도가 있었지만, 이 방법은 모든 사물마다 인간이 새로운 규칙을 만들어내야 했고, 다루기 힘들었기 때문에 방대한 세계의 사물을 인식하는 데에는 부적합했다.

따라서 방대한 양의 사물을 인식하여 분류하기 위해서 각각의 사물의 이미지 데이터를 많이 확보하고, 머신러닝을 이용한 학습을 통해 기계가 처음보는 이미지 속의 사물을 인식하도록 하는 방법을 사용했다. 머신러닝을 이용한 모델에는 두 함수가 존재하는데, 하나는 Data와 Label을 제공하여 Classifier를 학습시키는 Train function, 나머지 하나는 Classifier에 새로운 Image data를 제공한 뒤, label를 맞추는 Predict function이다. 이 방법이 과거 20년간 주류가 된 방법이다.

가장 간단한 Image Classifier - Nearest Neighbor Algorithm
- Train Step : 새로운 규칙을 생성하는 것이 아닌 데이터 저장이 최근접 알고리즘의 훈련단계이다.
- Predict Step : 저장된 이미지 데이터들 중에서 입력된 이미지 데이터와 가장 비슷한 데이터의 Label을 부여한다.
- 대표적인 DataSet으로는 CIFAR10 데이터셋이다.
- Nearest Neighbor Algorithm이 저장된 이미지들과 입력된 이미지들을 비교하기 위해서 사용하는 방법은 L1 Distance 방법이다. 이 방법은 각각의 Pixel Value의 Absolute값을 다 더한 값을 이용하는 방법이다.
- Nearest Neighbor Algorithm의 Full Python code는 다음과 같다.
- ```
import numpy as np
        
class NearestNeighbor:
	def __init__(self):
	pass
    	
	# Memorizing training data
	def train(self, X, y):
	self.Xtr = X
	self.ytr = y
    	
	# Finding the most similar image 
	def predict(self, X):
		num_test = X.shape[0]
		Ypred = np.zeros(num_test, dtype = self.ytr.dtype)
    	
		for i in xrange(num_test):
			distances = np.num(np.abs(self.Xtr - X[i,:]), axis = 1)
			min_index = np.argmin(distances)
			Ypred[i] = self.ytr[min_index]
    		
	return Ypred
```
- 최근접 이웃 알고리즘의 경우는 n개의 예시가 존재한다면, Train 과정에서 O(1), Predict 과정에서 O(n)의 시간이 걸린다. [Big-O notation] 하지만, 이는 예측과정이 훈련과정보다 훨씬 더 긴 시간이 걸리기 때문에, 활용도가 떨어진다는 단점이 있다. - CNN 알고리즘의 경우 역전이 가능
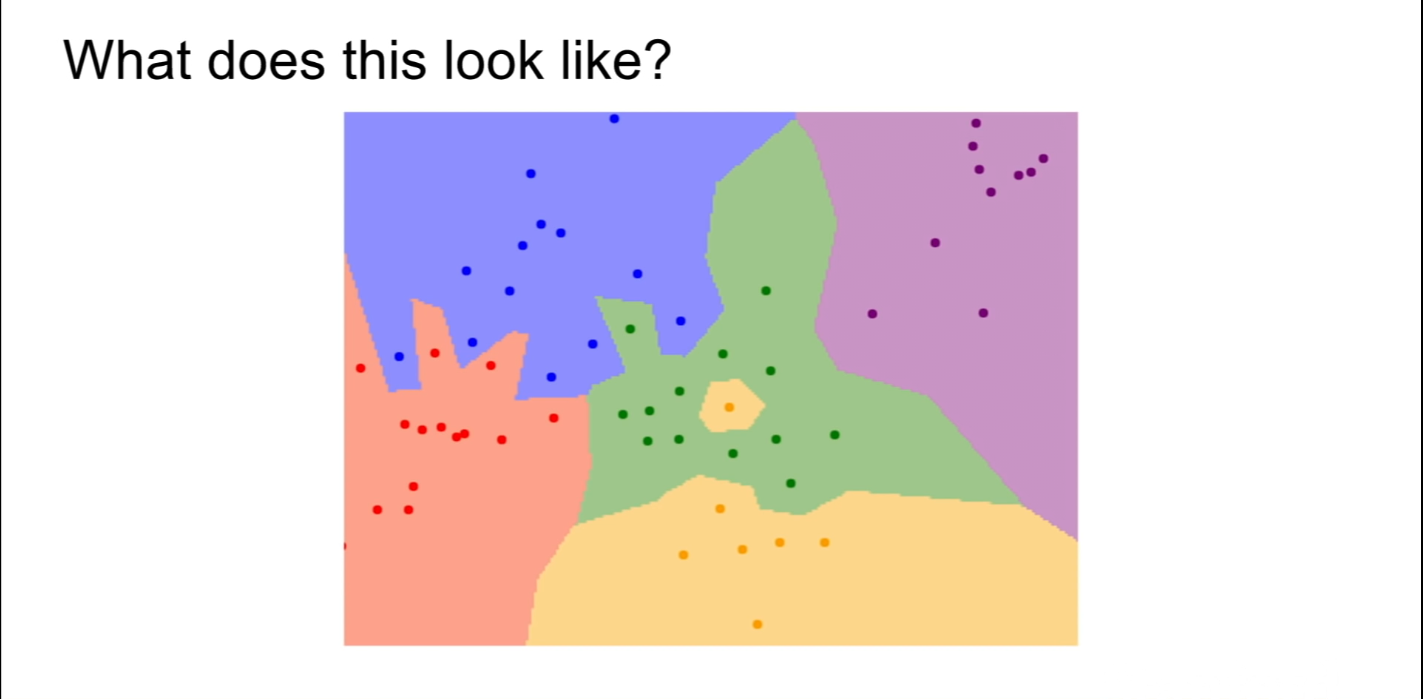
- 또한, Nearest Neighbor 알고리즘의 경우에는 가장 가까운 데이터셋의 레이블을 그대로 따라가기 때문에 특이한 데이터값이 레이블링에 큰 영향을 미치고, 아래와 같은 그림처럼, 영역의 분류가 난해하거나 제대로 이루어지지 않을 수 있다.
Nearest Neighbor Algorithm을 보완하는 K-Nearest Neighbor Algorithm
- Nearest Neighbor Algorithm과 비슷하게 Predict Image와 가장 가까운 Data를 판단하는 것은 동일하지만, 단 하나의 Data만을 이용하는 Nearest Neighbor Algorithm과는 달리 K-Nearest Neighbor Algorithm은 Test Image와 가장 가까운 K개의 데이터를 추출한 뒤, 대다수를 차지하는 레이블을 부여하는 방식이다.
- 실제로 영역 분류가 난해하거나 제대로 이루어지지 않는 Nearest Neighbor Algorithm과는 다르게, K-Nearest Neighbor Algorithm의 경우, K가 늘어남에 따라서 경계가 점점 더 명확해지는 것을 확인할 수 있다.
  
  위 사진의 White space는 여러 레이블과 Distance가 동일하기에 판단이 불가능한 구간이다.

Distance Metric

Nearest Neighbor Algorithm이나 K-Nearest Neighbor Algorithm를 사용하는 경우, Test Image의 데이터와 가장 비슷한 데이터를 찾기 위해 Pixel 별로 차이를 계산해야 한다. 이때, 데이터의 차이를 계산하는 방법에는 총 2가지가 존재한다.

하나는 이미지 데이터 차의 절대값만을 이용하는 d1(Manhattan)방식과 실제 이미지 데이터들의 픽셀 값의 직선거리를 이용하는 d2(Euclidean)방식이 존재한다. 각각의 수식은 아래과 같다.

Hyperparameter

Hyperparameter(하이퍼파리미터)는 일반적인 파라미터와 달리 어떤 값을 기준으로 인공지능을 학습시킬 지를 결정하는 것을 의미한다. K-Nearest Neighbor Algorithm로 예를 들면, 어떤 K값을 설정할 것인지, 거리를 측정하는 방법은 어떤 것을 사용할 것인지를 결정하는 것을 Hyperparameter라고 한다.

Hyperparameter는 문제에 따라서 효율적인 값들이 달라지기 때문에, Problem-dependent(해결해야하는 문제에 따라서 Hyperparameter는 달라진다)하다. 따라서 여러 hyperparameter값을 이용하여 가장 효과적인 값들을 찾아야 한다.

Hyperparameter 결정

어떤 hyperparameters가 데이터셋에 가장 효과적인지를 테스트하려면, 먼저 가지고 있는 DataSet을 잘 분류해야 한다.
- Data Set = Train Data
  
  이 경우, Data Set 안에 속해 있는 Predict Data의 경우, 항상 완벽하게 예측이 가능하나, 이는 정답을 알고 시험을 보는 것처럼 전혀 의미가 없다.
- Data Set = Train Data + Test Data
  
  이 경우, 여러가지 Hyperparameters를 Train data를 이용하여 학습시킨 뒤에, Test Data로 가장 높은 성능을 보이는 Hyperparameter를 고를 수 있을 것처럼 보인다. 하지만, 우리가 확인해야하는 Data는 머신러닝 모델이 한번도 보지 못한 데이터이기 때문에, Unseen Data를 가지고 테스트를 하지 못하는 이 경우도 의미가 없다.
- Data Set = Train Data + Validation Data + Test Data
  
  이 경우, Train data를 이용하여 모델을 학습 시키고 Validation Data를 이용하여 어떤 hyperparameter가 가장 좋은 성능을 보여주는지를 판단하고, 마지막으로 Unseen Data에 해당하는 Test Data로 선택한 hyperparameter의 성능을 평가하기 때문에 가장 적절한 방법이라고 볼 수 있다.
- Cross - Validation
  
  Cross Validation의 경우에는 Data Set에서 Test Data를 분류해두고, Train Data와 Validation Data를 여러가지 방법으로 분류한 뒤에 이들 각각의 예를 학습시켜 어떤 hyperparameter 성능이 더 좋은 지에 대해서 더 분명하게 파악할 수 있게 해준다. 다만, 머신러닝에서는 잘 쓰이지 않는 방법이다.

K-Nearest Neighbor Algorithm의 사진 분류에 있어서의 한계점

이 알고리즘은 사진을 분류하는 문제에 있어선 거의 쓰이지 않는다. L1, L2 거리 측정법이 이 경우에선 hyperparameter가 아니기 때문이다.
Curse of dimensionality - K-Nearest Neighbor Algorithm은 어떤 규칙을 찾는거나 추정하는 것이 아니기 때문에 정화도를 향상시키려면, 밀집도가 높은 Training point가 필요하다. 사진을 인식하기 위해서 사용하는 레이블은 단순한 차원이 아니기 때문에 높은 차원을 이용할 수 밖에 없고, 이를 위해선 엄청나게 많은 이미지 데이터가 필요하지만, 쉽지 않기 때문에, 사진 분류에서는 잘 쓰이지 않는다.

Linear Classification

Linear Classification은 CNN의 설계의 기초가 된다.
Parametric Approach

Linear Classification은 Parametric Model을 이용한다. Parametric Model에는 우리가 사용할 Input data와 Parameter나 Weight로 불리는 가중치 W를 사용한다. Linear Classification의 경우에, Parametric Model은 Wx+b의 형태의 선형성을 가지는 모델이 사용된다.

Parametric Approach의 경우 K-Nearest Neighbor Algorithm에는 그저 데이터를 저장하는 것에 그쳤다면, Parametric Approach의 경우는 Train Data를 이용하여 W(가중치)를 더 정확하게 하는 것을 목적으로 Training이 진행되기 때문에, KNN 알고리즘과 달리 Predict 시에 전체 Train Data가 필요하지 않고 W matrix만이 필요하다는 장점이 있다. Parametric Approach의 경우, 가중치 W와 Data X, 그리고 bias Data B를 적절히 조합하는 것이 가장 중요하다.

이 중에서 가장 간단한 것이 Linear Classifier인데, 이때의 Parametric Model function F는 F = WX로 표현된다. 가중치 W와 data X 모두 행렬이다. X행렬의 경우, Pixel value가 나열되어 있는 (number of data) x 1의 열벡터(Column Vector)로 표현되고, W 벡터의 경우는 (number of class) x (number of data)의 행렬로 표현이 된다.

예를 들어 32x32 픽셀의 RGB 정보를 가지고 있다면, 총 3072개의 data를 가지고 있다고 볼 수 있고, 10개의 카테고리로 분류하는 CIFAR10 DataSet라면, W는 10 x 3072행렬, X는 3072 x 1의 행렬로 볼 수 있다.

위의 사진에서 볼 수 있듯이, W 행렬의 각각의 Row matrix는 각각의 Category score과 관련이 있다. Row matrix와 data Column matrix의 내적이 바로 해당 카테고리의 score값이 되기 때문이다. 옆의 Bias matrix는 Data Independence를 나타내기 위해서 사용한다.

Parametric Model의 경우, W matrix를 통해서 역으로 Category별로 어떤 이미지를 해당 Category로 분류하는 지를 엿볼 수 있다. 이때, W matrix의 카테고리별 Row가 각 Label의 기준 Pixel data를 나타낸다. 다만, Linear Classification의 경우 하나의 row matrix만을 이용하기 때문에 정확한 이미지를 얻기는 힘들다.

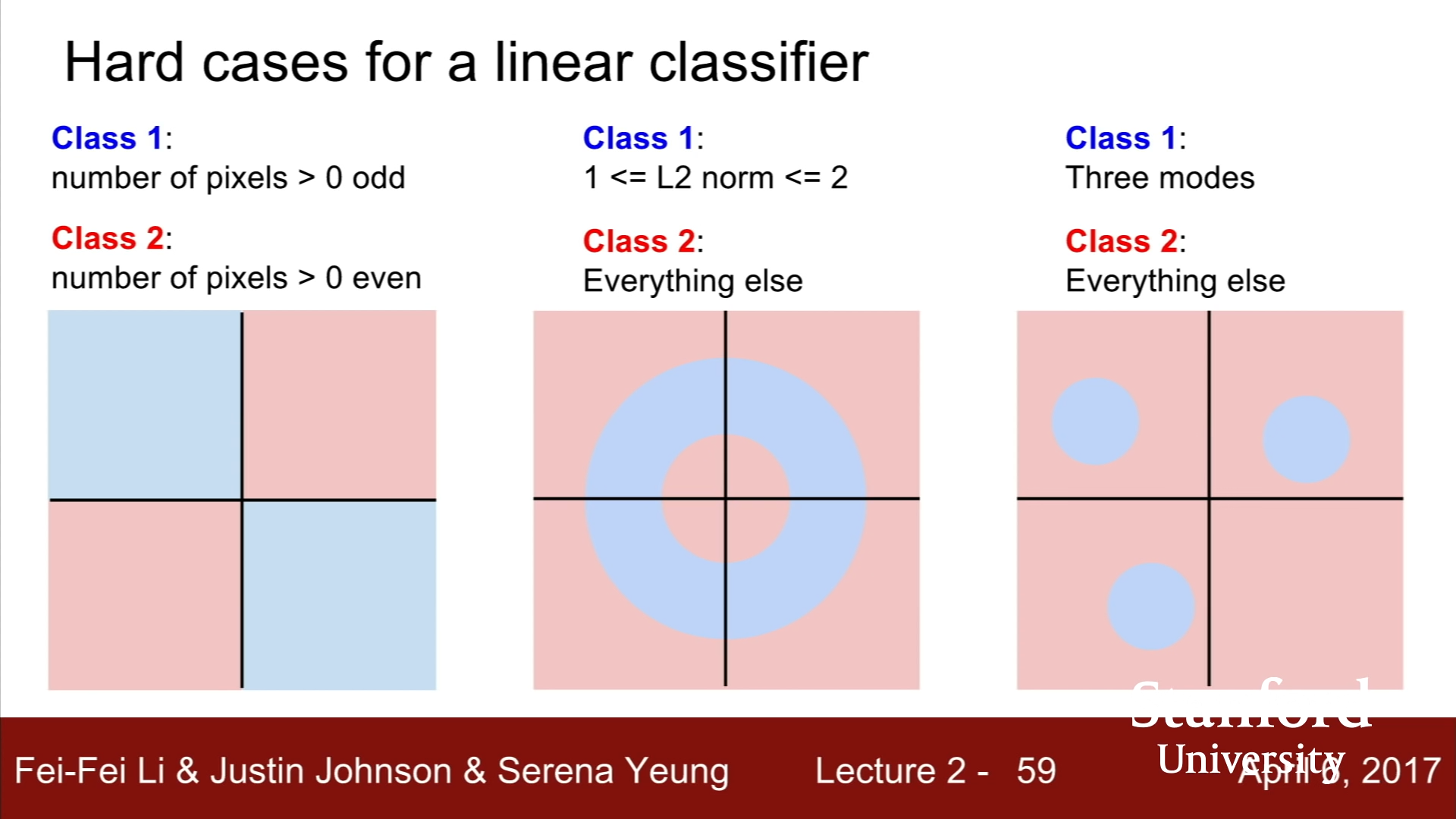
다만, Linear Classifier가 제대로 작동하지 않는 경우도 존재한다. 뒤의 그림과 같이 Case의 분류가 이분법적이고 선형적이지 않는 경우에 Linear classification으로는 제대로 나누어지지 않는다.

Summary

이번 강의에서는 Image Classification에 대해서 개략적인 소개와 가장 간단한 알고리즘인 NN알고리즘과 KNN알고리즘, 마지막으로 CNN 설계의 Building Block에 해당하는 Linear Classification에 대해서 다루었다. Linear Classification에 대한 내용은 다음 장에서 더 자세히 다루니, 파이썬을 이용한 KNN 실습을 시도해보아야겠다.

CS231n - Lecture 2

#2 - Image Classification

Further Reading

CS231n - Lecture 1

CS231n - Lecture 3

CS231n - Lecture 4