Home CS231n - Lecture 3
Post
Cancel

CS231n - Lecture 3

Posted Sep 2, 2023
By 전형준
24 min read

#3 - Loss Functions and Optimization

  • Review of #2 Lecture
  • Loss Function
  • Multi - Class SVM Loss function
  • Regularization
  • Softmax Classifier (Multinomial Logistic Regression)
  • Optimization
  • Image Feature
  • Review of #2 Lecture

Lecture 2에서 공부했던 Linear Classification에서 W 행렬의 각각의 행값에 대응되는 Score은 Label과의 유사도를 나타내는 지표가 된다. Function을 거쳐저 나온 각각의 값들이 높을수록 이것이 해당 Label과 더 유사하다는 것의 의미한다.

W 행렬에서 Scored의 가중치가 존재하는데 각 Row들의 숫자를 이용해 다시 이미지를 구성한다면, 학습한 Template를 확인할 수 있다.

image-20230827201128229

이전 강의에서는 Train data를 가지고 어떻게 W 행렬을 결정해야 하는 지에 대해서 다루지 않았다.

  • Loss function

Train을 진행하면서 W행렬값이 제대로 설정되어야 Label을 정확히 할당할 수 있다. 이를 위하여 현재 score가 얼마나 나쁜 것인지를 알 수 있어야 한다. W 행렬을 Input으로 가지고 얼마나 좋고 나쁜지를 판단해주는 function이 바로 Loss Function이다.

Loss function은 어떤 W행렬이 가장 최선의 선택인지를 확인해야 하기 때문에 최적화 과정 (Optimization Procedure)과도 연관이 있다.

3가지 Class로 분류를 하는 Toy Example을 살펴보자.

image-20230827223717551

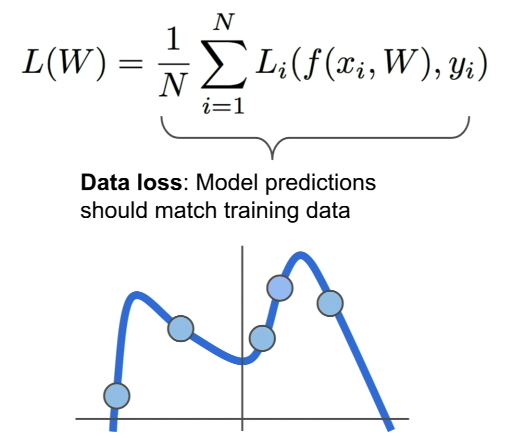
위의 예시에서는 차가 제대로 분류가 되었지만, 고양이와 개구리의 경우, 제대로 된 분류가 이루어지지 않았다. 이를 교정하기 위해서 Loss Function을 이용한다. N개의 Train data로 Machine을 훈련시키는 경우, N은 Train data의 개수가 되고, (xi, yi)는 이미지와 각각의 Train data의 레이블을 의미한다. 또한, 여기서 i는 Train data의 숫자를 임의로 설정한 것이다.

Loss Function의 결과값 각각은 Li로 나타내는데, Li의 매개변수로는 xi와 W를 가지고 예측한 Parametric Function의 결과(예측)값과 yi(실제)값들이 들어가고, 결과로는 예측값과 실제값이 얼마나 차이가 나는 지를 알려준다. L1~LN까지의 평균값을 Final Loss값으로 사용한다. 이는 머신러닝 훈련 과정에서 어떤 매게변수 설정 W를 사용해야 Train data를 가장 잘 활용할 수 있는 지를 알려주기 때문에 자주 사용되는 함수이다.

  • Multi - Class SVM Loss function

image-20230827235922956

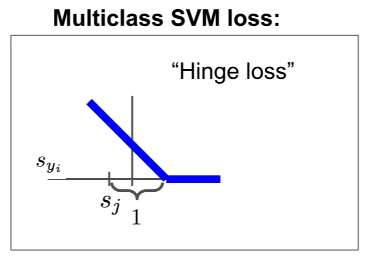
Multi Class SVM Loss function은 Loss function은 f(x,W)의 결과의 각 Category의 template를 고려할 때, 정답인 yi category template의 값을 s_yi로 표현하고, 나머지 categories의 점수를 s_j로 표현했을 때, s_yi가 sj+1 값보다 크거나 같은 경우에는 0, 작은 경우는 (s_j + 1) - s_yi의 값을 이용하여 N개의 j값을 더한 값을 Li로 이용한다.

image-20230828000530392

x축을 sj, y축을 syi로 표현한 그래프를 살펴보면, 최솟값은 0, 최댓값은 무한대로 발산하며 선형적인 분포를 띄고 있는 것을 확인할 수 있다. 이를 “Hinge Loss”라고 부른다.

image-20230828001118770

이를 위의 예시를 통해 확인하면, Cat Category의 경우, 나머지 Car Category의 점수 +1 보다 2.9가 작고 해당 값은 2.9이고, Frog Category의 경우에는 Frog Category 점수 +1 보다 Cat Category의 점수가 더 크기 때문에 0의 값을 가진다. 따라서 고양이 카테고리의 값은 2.9 + 0인 2.9가 된다. 나머지 방식으로 Car, Frog Category의 Li값을 계산하면, 각각 0과 12.9가 나오게 되고, Final Loss는 2.9, 0, 12.9의 평균인 5.27이 된다.

이때 정답인 카테고리 템플릿과 정답이 아닌 템플릿의 점수 차이인 1을 생각해본다면, 이 차이는 Loss function에서 W의 값에 전부 반영되어 1값이 아닌 다른 값을 사용한다고 하더라도, 정답인 template이 더 확실히 더 큰 score값을 가진다는 점이 필요한 것이지, 구체적으로 어떤 값을 사용해야 더 좋은 Loss function인지는 정해져있지 않다.

  • 의문점 1: 만약, 위 예시의 Car의 Score이 조금 달라진다면 Loss에 영향을 미칠까?

    • 만약 Car의 계산값이 0 초과의 값이라면, 조금의 변화도 값에 영향을 미칠것이지만, Cat과 Frog Category 전부 0값을 가지기에 별다른 영향을 미치지 못할 것이다.

  • 의문점 2: Multi-Class SVM Loss의 최댓값과 최솟값은 어떻게 될까?

    • 그래프에서 확인할 수 있듯이, 최솟값은 0, 최댓값은 무한대로 발산한다.

  • 의문점 3: Parametric Function의 결과값으로 나온 s값들이 전부 0에 수렴한다면, 어떤 Loss 값을 가질 것인가?

    • s값들이 0에 수렴한다면, 각각의 결과값은 1의 가질 것이므로, Li는 N-1의 Loss 값을 가질 것이다.

  • 의문점 4: 만약 Li의 값에 정답인 template의 score도 더해준다면, 어떻게 되겠는가?

    • 정답인 template 점수도 사용한다면, Loss값은 원래 값보다 1 큰 값을 가질 것이다.

  • 의문점 5: 만약 Li이 ((s_j + 1) - s_yi) ^2의 합을 사용한다면, 이는 Multi-Class SVM일 것인가? 다른 Loss function일 것인가?

    • 이 경우, 그래프를 확인하면, 선형적인 분포를 띄고 있지 않을 것이기 때문에, 이는 다른 Loss function으로 생각해야 한다. Squared Loss를 사용한다면, 우리가 Train한 값들과 실제 값들이 차이를 Hinge Loss 때보다 더 크게 인식하기 때문에, 더 많은 보정을 할 수 있게 해주는 장점이 있다. 이처럼 우리가 어떤 종류의 오류를 다룰 것인지에 맞추어 효율적인 Loss function을 선택해야 한다.

  • 의문점 6: Final Loss값이 0이 되는 W 행렬을 찾았을 때, 이 행렬 W가 과연 유일한 행렬일까?

    • 앞에서 말했듯, Hinge loss 구조에서는 최솟값이 0이므로, Final Loss 값이 0이라면, 각각의 Li값들 또한 0값을 가져야 한다. 이는 다시말해, 각각의 max (sj - syi + 1) 값들이 전부 0의 값을 가져야 한다는 것을 의미한다. 따라서, sj - syi값이 -1보다 작거나 같다는 의미이고, W대신 nW(양의 정수 n배한 행렬 W)를 사용했더라도 max값이 0이 되므로 Final Loss 또한 0이 되고, 이는 유일한 행렬이 아니다.
    • Machine learning에서 가장 중요한 점은, 이미 제공된 Training Data에 알고리즘을 맞추는 것이 아니라, 새로운 Unseen Test Data들에 대한 Prediction을 잘해야 한다는 점이다.

    image-20230828004927614

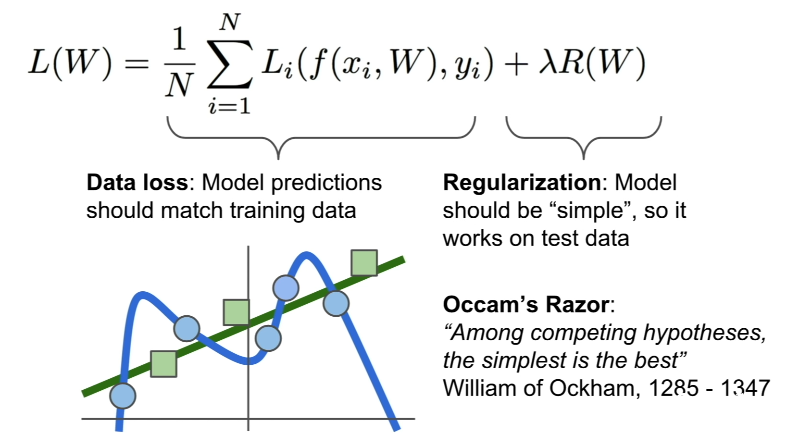
    • 위의 예시처럼, Train data를 가지고 이에 완벽하게 들어맞는 Model을 만드려고 하는 경우, 어지러운 곡선의 형태를 띄게 될 것이고, 이는 Test data를 가지고 테스트하려는 목적과는 맞지 않는다.

    image-20230828005309058

    • 이에 대한 문제를 해결하기 위해 Loss Function에는 앞에서 살펴본 Data Loss 부분 이외에도 Regularization(정규화)와 관련된 부분들 또한 존재한다. 이를 통해서 간단한 선형적인 Model로 정규화시켜주어야 Test Data의 Prediction에 맞게 변형시킬 수 있다.

    • 1
2
3
4
5
6
7

      # 아래 코드는 SVM Loss funtion을 간단히 표현한 Python 코드이다.
def L_i_vectorized(x, y, W):
    scores = W.dot(x)
    margins = np.maximum(0, scores - scores[y] + 1)
    margins[y] = 0
    loss_i = np.sum(margins)
    return loss_i
  • Regularization

실제로 사용되는 정규화에는 여러가지 종류가 존재한다.

L1, L2 Regularization, Elastic net Regularization, Max norm Regularization…

이 중에서 가장 일반적인 정규화는 L2 Regularization으로, W 벡터의 L2 Norm에 해당하는 값이다.

이와 비슷하게 L1 Regularization의 경우는 W 벡터의 L1 Norm을 R(W)로 사용한다.

L1L2

L1과 L2 Regression의 경우는 복잡도를 측정할 수 있다.

위의 예시에서 볼 수 있듯이, L2 Regression은 L2 Norm을 이용하기에 W의 원소들 중에서 0이 많은 경우보다 0이 적은 경우를 선호하는 것을 알 수 있다. 위의 예시에서는 차이가 없지만, 일반적으로 L1 Regression은 L1 Norm을 이용하기에 W의 원소들 중에서 0이 더 많은 Sparse solution을 선호한다.

따라서 L2의 경우에는 Zero-Component가 많을수록 값이 더 퍼져 있을수록 복잡도가 더 높다고 간주하고, L1의 경우에는 Zero-Component가 더 많을수록 복잡도가 더 낮다고 간주한다.

Q. Regularization을 더한다고 해서 Polynomial model이 Linear하게 변하지 않는다.

물론 다항회귀가 선형회귀로 변하지는 않지만 Polynomial Regression의 확장 개념으로 생각한다면, Polynomial Regression 시에 가져야 할 계수를 통제하여 간단한 형태로 바꾸는 것으로 볼 수 있다.

  • Softmax Classifier (Multinomial Logistic Regression)

Multi - Class SVM Loss function은 Score에 대한 해석이 존재하지 않고, 단지 정답 Class와 오답 Class의 정답이 일정 크기 이상 차이만 나도록 조정했었다.

Softmax Classifier (Multinomial Logistic Regression)는, 반면에 Score을 사용하여 확률 분포를 형성한 후, 이를 학습에 이용한다.

image-20230902173147252

Softmax classifier의 경우에는, Score의 값들의 exponentiate값을 이용하여 전체를 양수로 만들고, 각 Class들의 이 값들을 이용하여 정규화시킨 뒤, 이를 이용하여 확률분포를 만든다. 모델 학습을 통해서 원하는 것은 확률분포가 정답인 Class는 1의 확률을 가지고, 나머지 오답인 Class는 0을 가지도록 하는 것이다.

확률 분포를 더 쉽게 이용하기 위해서 상용로그함수의 값을 이용할 것이고, log함수의 특성에 따라서 -값을 붙여 Loss값을 계산한다.

image-20230902174716745

실제 예시를 들면 위와 같은 형태로 계산이 된다. SVM과 다른 또 하나의 지점은, SVM의 경우, 오답인 Class의 개수만큼의 값들의 합으로 Li값이 계산되었지만, Softmax Classifier의 경우에는, 정답인 확률값만을 이용한다는 점이다.

  • Q1. Loss값의 최대와 최소는 어떻게 될까?
    • 확률이 0에서 1사이이기 때문에, -log값은 0부터 무한대까지이다.
    • 학습을 통해서 도달하고자 하는 최종 목적지인 정답이 1이고, 나머지 오답은 0의 확률을 위해서는 , e^x의 값이 0과 1이 되어야 하므로, 정답인 score은 양의 무한대의 값, 오답인 score은 음의 무한대의 값을 가져야 한다. 하지만, 컴퓨터는 무한대를 잘 다루지 못하므로 최대한 큰 값을 이용하게 된다. 그러므로 완전한 1과 0의 값은 사용하지 못한다.
  • Q2. 전체 Score값이 전부 0에 수렴한다면, Loss값은 어떻게 될 것인가?
    • Li값은 -log(1/n)이므로 logn의 값을 가질 것이다. (이때, n은 Class의 개수이다). 이를 이용하면, score가 존재하지 않은 초기치에서 설계가 제대로 되었는지 디버깅 하는 데에 사용할 수 있다.
  • 추가적인 차이점
    • SVM Loss function을 이용하는 경우, 정답 점수와 오답 점수 간에 일정한 차이만 존재한다면, 목표를 달성했다고 간주하고, 더 진행하지 않지만, Softmax Classifier를 이용하는 경우, 계속해서 정답인 확률을 1에 가까이 가도록 학습하기 때문에 계속해서 학습이 진행된다.
  • Optimization

Loss가 최소가 되도록 하는 W를 실제로 어떻게 찾는 것인지를 생각하는 것이 Optimization(최적화)이다.

  1. Random Search

​ 무작위로 어느 지점이 가장 Loss가 작은 W인지를 골라 Test해보는 방식이다.. 하지만 쓸모가 없다.

  1. Derivate값을 이용(미분값)

​ 기울기가 최소인 방향을 계속 진행하다 보면, Loss가 가장 작은 지점에 도달할 것이라는 생각을 이용한다.

  • Derivative of W(dW)

간단히 말해서 일차미분값을 이용하여 slope를 계산한다. 이는 다변수함수에도 적용이 되므로, 다변수함수의 경우에는 편미분을 이용하여 기울기를 계산할 수 있고, 전체 방향에서의 기울기를 알기 위해선 unit 벡터와 미분의 내적으로 구할 수 있다.

  • 기울기 계산

Derivate

위의 방법처럼, Loss function의 값을 이용하여 W의 기울기를 구할 수도 있으나, 이는 모든 W의 원소들에 대해서 한번씩 계산을 거쳐야하고, 정확한 미분값을 계산할 수도 없다는 단점이 있다.

image-20230902224024664

또 다른 방식은, 미적분을 이용한 Analytic Gradient를 이용하는 방식이다. 이는 실제 수치적인 계산보다 훨씬 빠르고 정확하다는 장점이 있다.

따라서 실제로 이를 사용하는 경우에는 언제나 Analytic Gradient를 사용하고, Debugging tool로써 Numerical Gradient을 사용하는 방식으로 사용한다. 이를 Gradient Check이라고 부른다.

  • Gradient Descent
  1. W를 랜덤한 값으로 초기화시킨다.
  2. dW를 계산하여 Updated Weights = - Original Weights - (Step size) *(dW)를 계속해서 반복한다.

이를 코드로 나타내면 아래와 같아진다.

1
2
3

while True :
    weights_grad = evaluate_gradient(loss_fun, data, weights)
    weights += -step_size * weights_grad

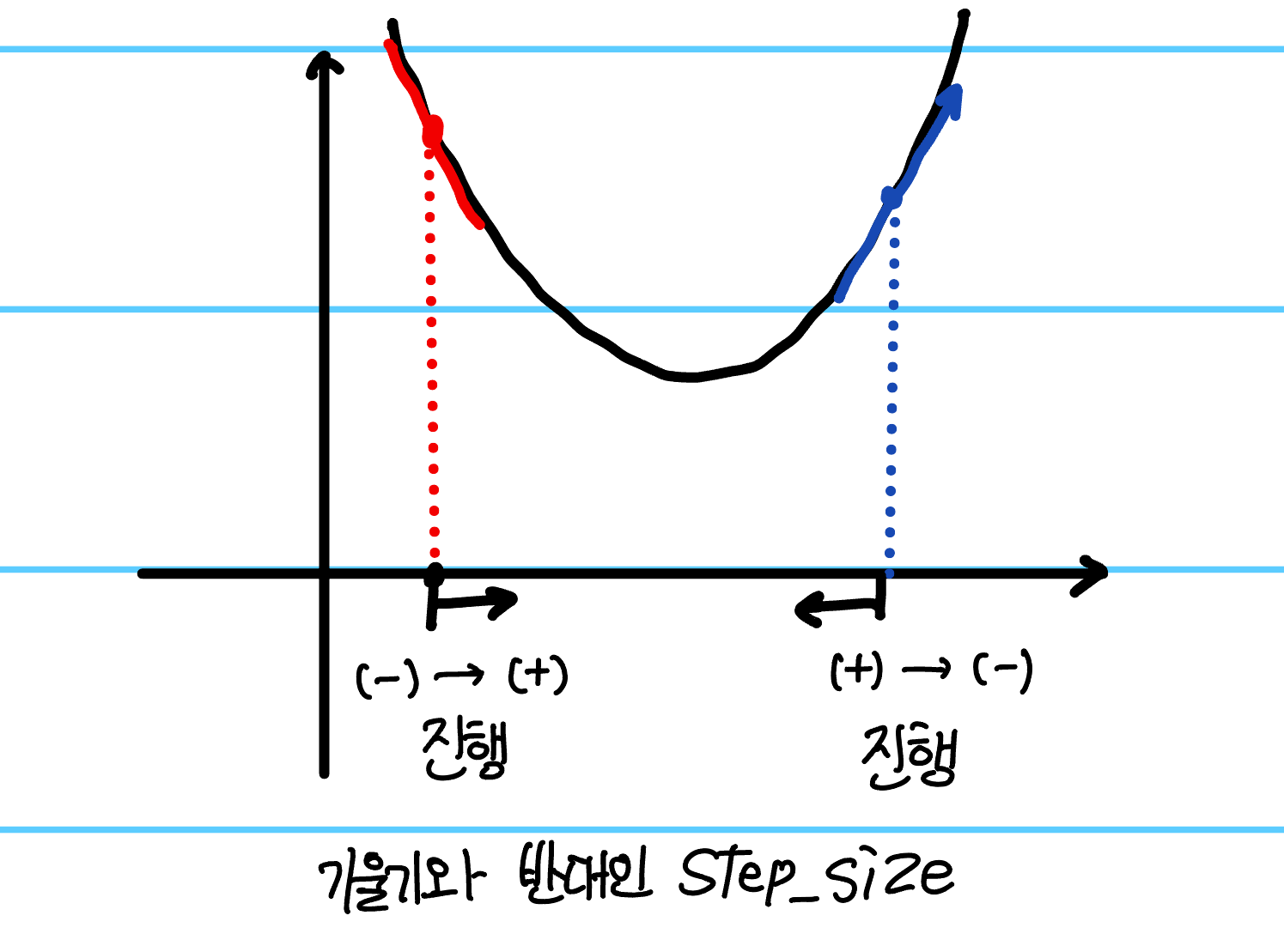
위 코드에서 - 값을 붙여서 더해주는 이유는 양의 기울기를 가지는 경우, 음의 방향으로 진행해야 최저에 도달할 것이고, 음의 기울기를 가지는 경우, 양의 방향으로 진행해야 최저에 도달할 것이기에 이를 붙여주는 것이다. 이를 그림으로 표현하면 아래와 같다.

direction

이때, Step_size는 Hyperparameter로, 각 문제에 따라서 적절한 Step size를 고려하는 것이 중요하다.

  • Stochastic Gradient Descent

image-20230902233727912

전체 Training data의 Loss를 실제로 구하고, 이를 다시 학습시키는 것은 너무나 많은 자원과 시간이 필요하다. 따라서 매 반복마다, Minibatch라고 불리는 32/64/128개 등등의 training example를 뽑아서 전체 sum을 추정하여 loss값을 추정하는 데에 사용한다.

1
2
3
4

while True :
    data_batch = sample_training_data(data, 256)
    weights_grad = evaluate_gradient(loss_fun, data_batch, weights)
    weights += -step_size * weights_grad

위의 코드에서, Vanilla Gradient Descent와 다른 단 한가지는. training data 전체가 아니라 일부를 이용한다는 것이다.

  • Image Feature

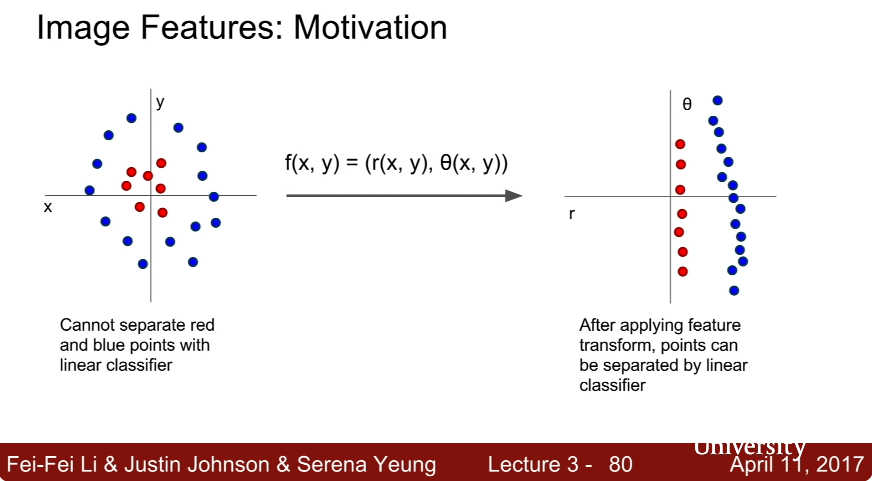
Linear Classification에서는 Raw Image Data 전체를 이용하여 이와 관련된 모델을 학습시켰지만, 이는 그다지 효율적인 방법이 아닐 수 있다. 각 특징별로 필요한 데이터를 추출한 후, 이 데이터를 이용하여 Linear Classification을 진행시킨다면, 더 효율적이고 정확한 방식으로 이미지를 인식할 수 있을 것이다.

image-20230902235622446

위 그림처럼 Linear Classification으로 학습할 수 없는 것처럼 보이는 것들도 Feature Transform을 진행한다면, Linear Classification으로 해결할 수 있게 된다.

Feature Vector의 종류

  1. Color Histogram : 어떤 색깔이 Image data에서 어느 분포로 존재하는지에 대해서 histogram으로 나타낸 것이다.
  2. Histogram of Oriented Gradients : 이미지의 pixel에서 각 8x8짜리 영역에서 어떤 모서리 정보가 가장 두드러지게 존재하는지를 파악하여 그림으로 나타낸 것이다. Color Histogram은 색에 대한 전체적인 정보를 담고 있고, Feature Vector의 경우에는 지역적으로 어떤 방향의 모서리가 주가 되는지에 대한 정보를 담고 있다.

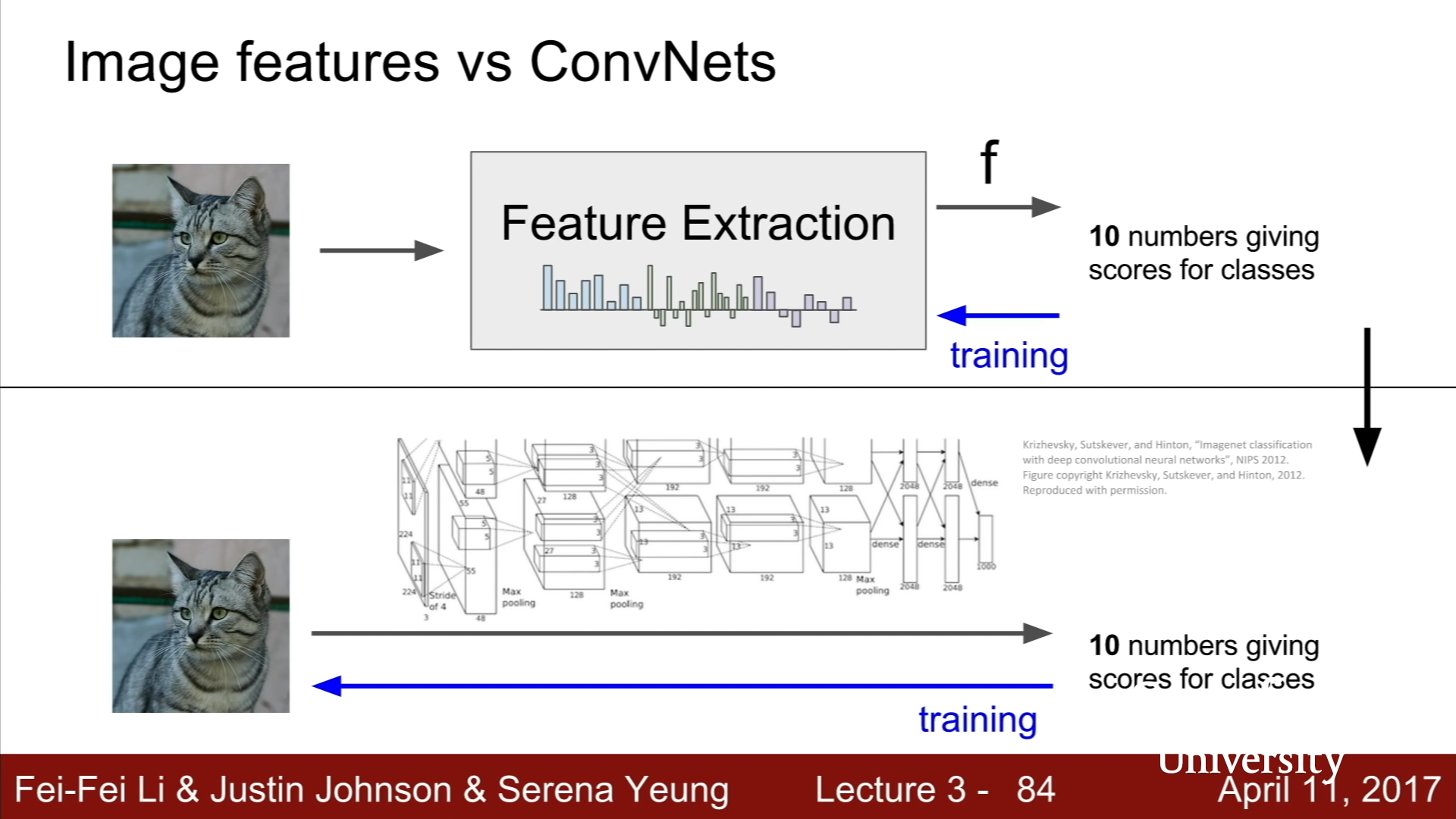
image-20230903001505070

Image Feature 방식의 경우는, Feature Extraction이 한번 진행되었다면, 그 특징 정보를 바탕으로 Linear Classifier를 계속 학습하고, Extraction을 다시 진행하지는 않는다. 반면, Convolutional Networks의 경우에는, 특징을 우리가 사전에 추출하는 것이 아니라, 학습 과정에서 특징을 알아서 학습하고 여러 종류의 계층을 거쳐 Linear classifier만의 가중치가 아닌 전체 가중치를 바꾼다는 차이점이 있다.

Study, Computer Vision
CV CS231n
This post is licensed under CC BY 4.0 by the author.
Contents