CS231n - Lecture 4

#4 - Introduction to Neural Networks

Analytic Gradient for Arbitrarily Complex Functions
Backpropagation
- What is backpropagation
- Patterns in backward flow
- Gradients for vectorized code
Modularized Implementation : Forward/Backward API
Neural Network
Neural Network & Activation function

Analytic Gradient for Arbitrarily Complex Functions

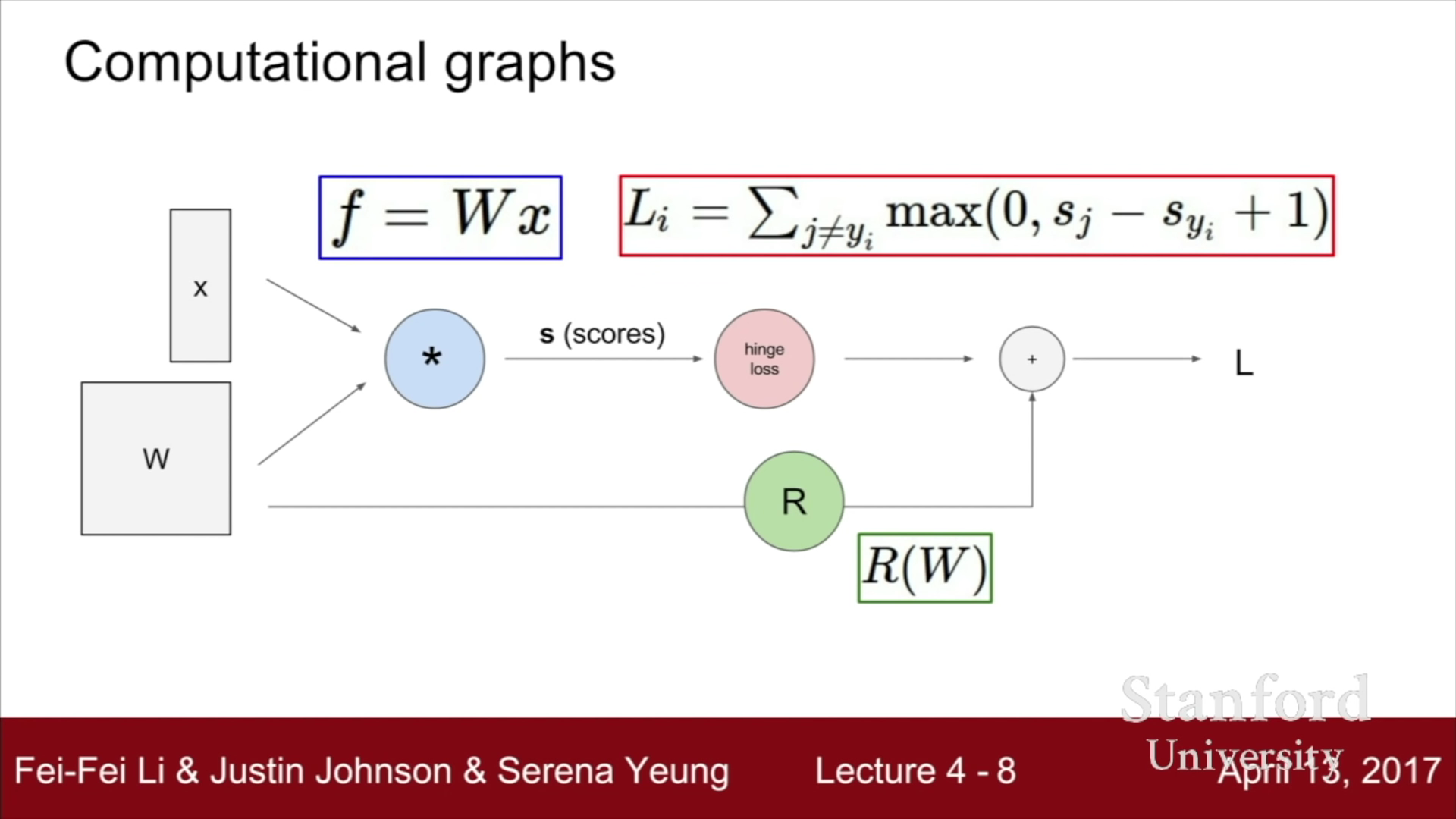
Analytic Gradient를 구하기 위해선 Computational Graphs를 사용해야 한다. Computational Graph는 우리가 사용하는 어떤 함수이던지 간에 그래프 상의 노드로 표현할 수 있다. 이전에 공부했던 Linear Classifier를 사용한 SVM Loss Function을 Computational Graph를 사용하여 나타내면 아래와 같다.

위의 사진에서 볼 수 있는 것처럼, 연산에서 사용하는 모든 함수들(곰셈, Max, 덧셈, Norm 연산)이 각 Node에 들어있고, 이를 링크시키는 선들로 그래프가 구성된다. 각 링크들은 한 단계 진행을 의미한다.

Backpropagation

위에서 Computational graph로 연산을 나타냈다면, 이와 함께 편미분의 연쇄법칙을 이용하여 Computational Graph의 모든 변수에 대한 기울기를 전부 구해낼 수 있다. 이 과정을 Backpropagation이라고 부르며, Neural Turing Machine 등 복잡한 Neural Machine에까지 널리 사용된다.

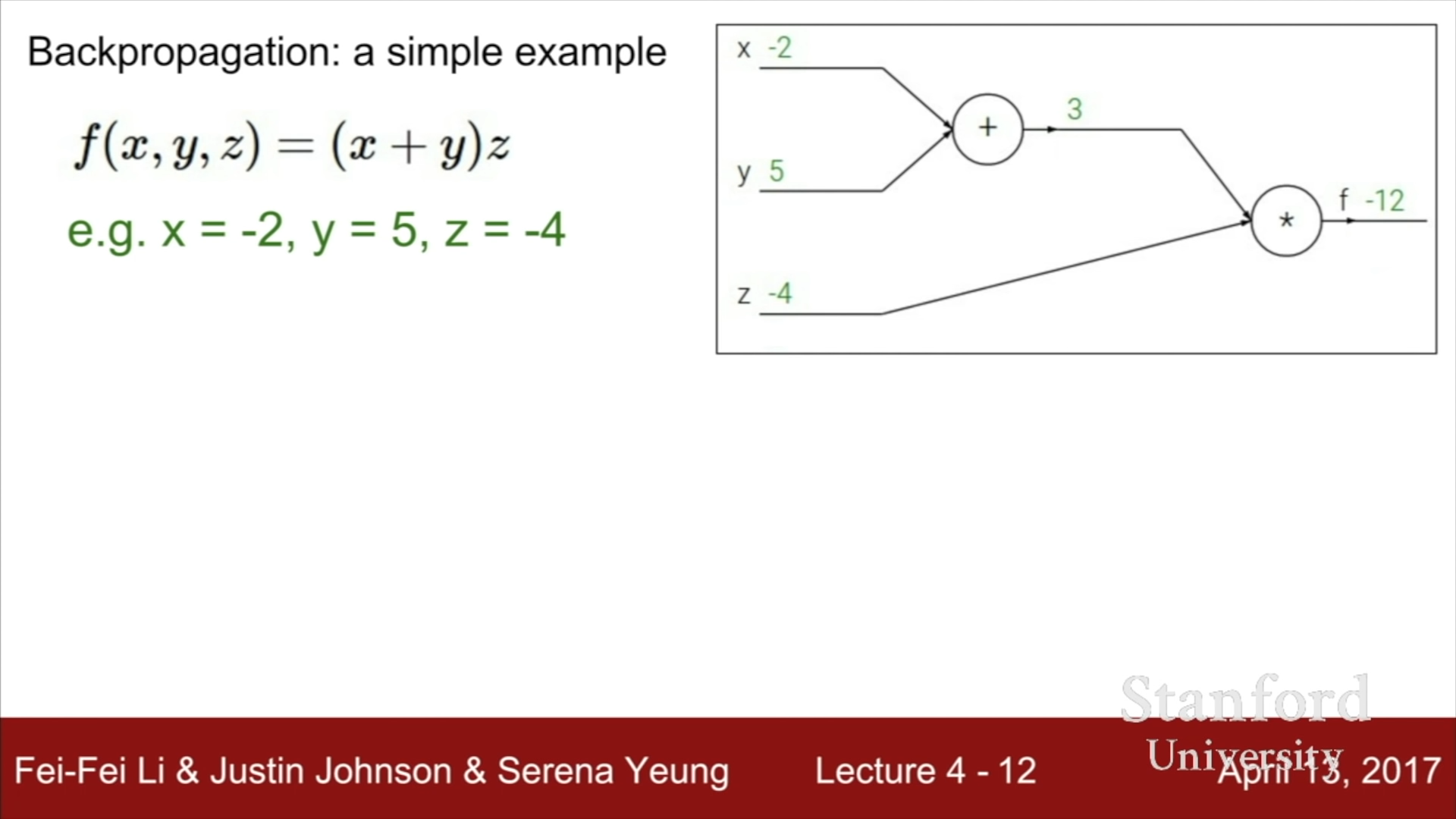
간단한 예시를 들어보자.

f(x,y,z) = (x+y)*z 함수의 Computational Graph를 그려본다면, 아래와 같다. (단, x+y = p라고 두자)

편미분을 사용하여 각 변수의 미분값을 구하려면, 다음과 같은 수식을 사용하면 된다.

위 수식처럼 편미분의 연쇄법칙을 사용하지 않고, f 수식을 풀어 직접 x,y,z에 대한 편미분을 각각 계산하여도 값 자체는 동일하지만, 수식이 아무리 복잡해도 위와 같은 방법을 사용하면 무조건 해결할 수 있고, 복잡한 계산을 간단하게 만들어준다는 점에서 장점이 있다.

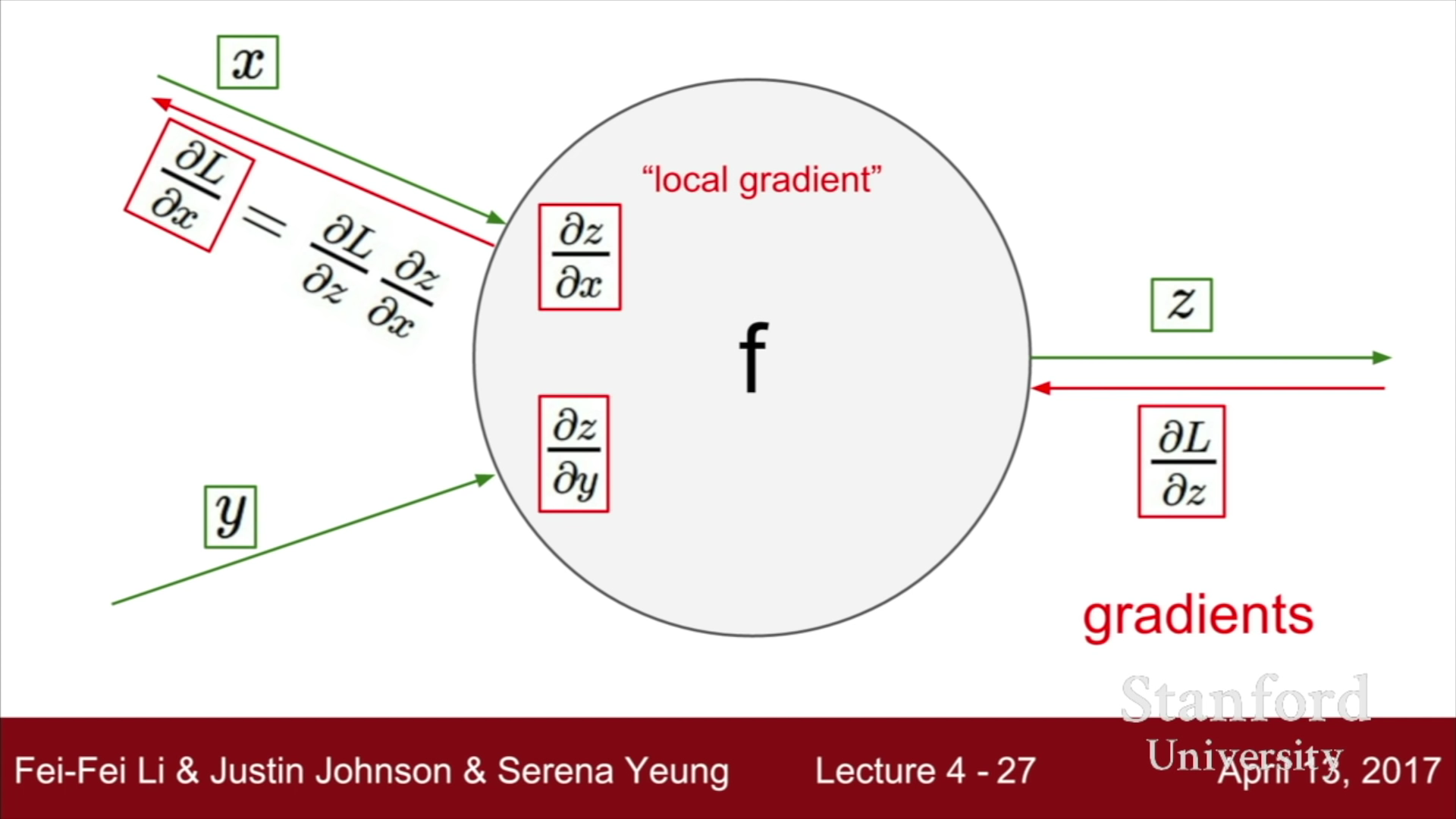
이를 간단히 정리하자면, 위의 그림으로 나타낼 수 있다. 상위 Layer의 기울기를 받고, 현재 layer의 편미분값만을 안다면, 단순한 곱셈만으로도 복잡한 미분을 하지 않고, 현재 Layer variable들의 편미분값을 구할 수 있다.

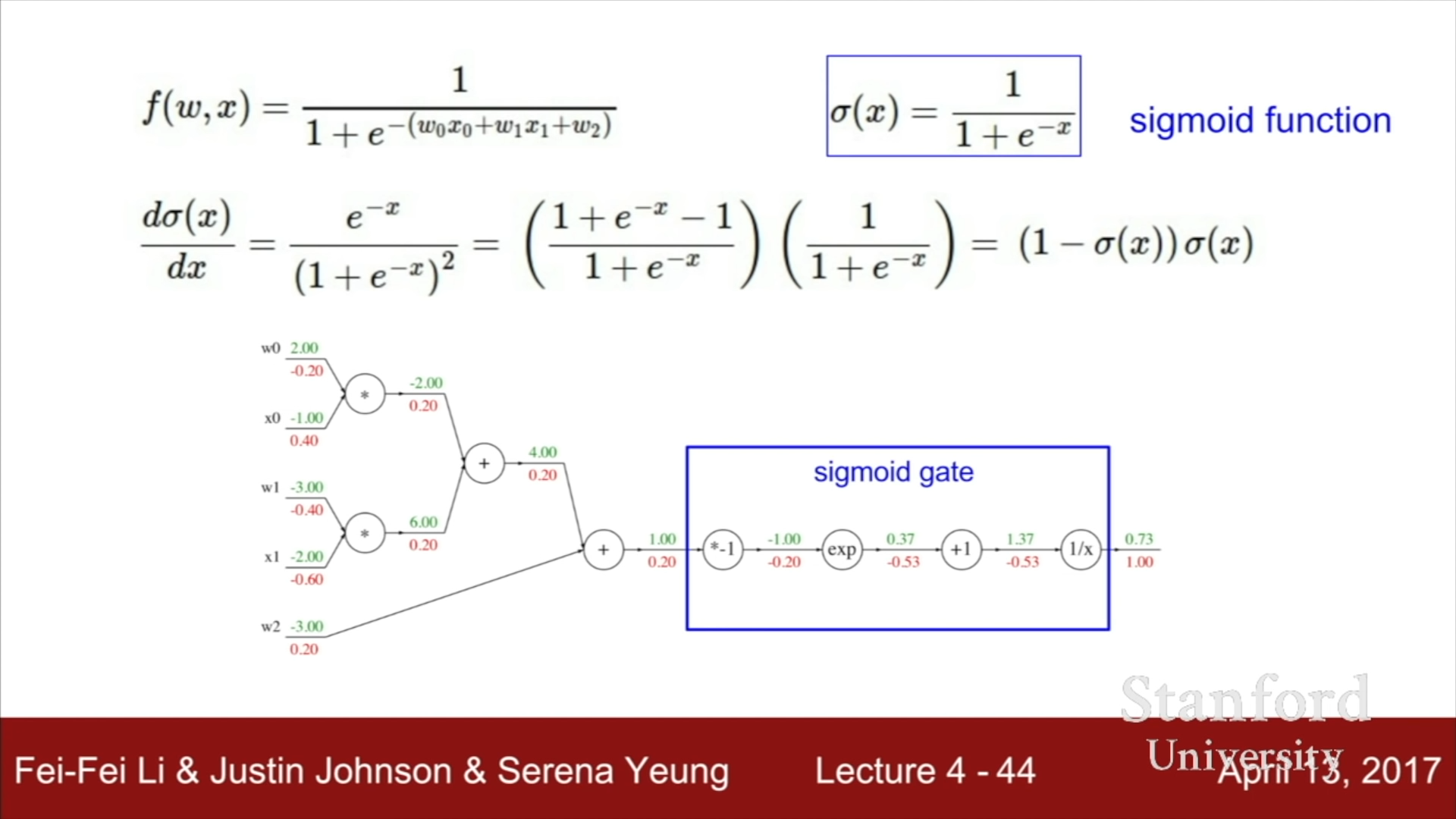
아래와 같은 복잡한 예시더라도, Computational Graph를 그린 뒤, 각각의 partial derivate들을 곱해간다면, 값들을 손쉽게 구할 수 있다.

Computational graph는 가장 간단한 함수들로 node를 구성했었지만, 여러 연속된 node들이 합쳐저 쉬운 partial derivate값을 만들 수 있다면, 이를 하나의 gate로 묶어서 사용해도 무방하다. 다시 말해, 얼마나 단순한 계산을 할 것인지는 설계 과정에서 설계자 본인이 선택하는 것이다.

Patterns in backward flow

Add gate : Gradient Distributor - f = x + y 인 경우, 편미분값은 x이든, y이든지 간에 1을 가진다. 따라서 이전 f에 대한 편미분값을 x와 y가 동일하게 가지는 것을 알 수 있다.
Max gate : Gradient Router - max gate의 경우, 두가지 중 한가지 변수값만을 온전히 가지므로, 선택된 하나의 변수만이 이전 변수에 대한 편미분값을 온전히 가지는 것을 알 수 있다.
Multiplication gate : Gradient Scaler - 이전 변수에 대한 편미분값을 x배로 하여 현재 노드의 변수에 대한 값으로 가진다.

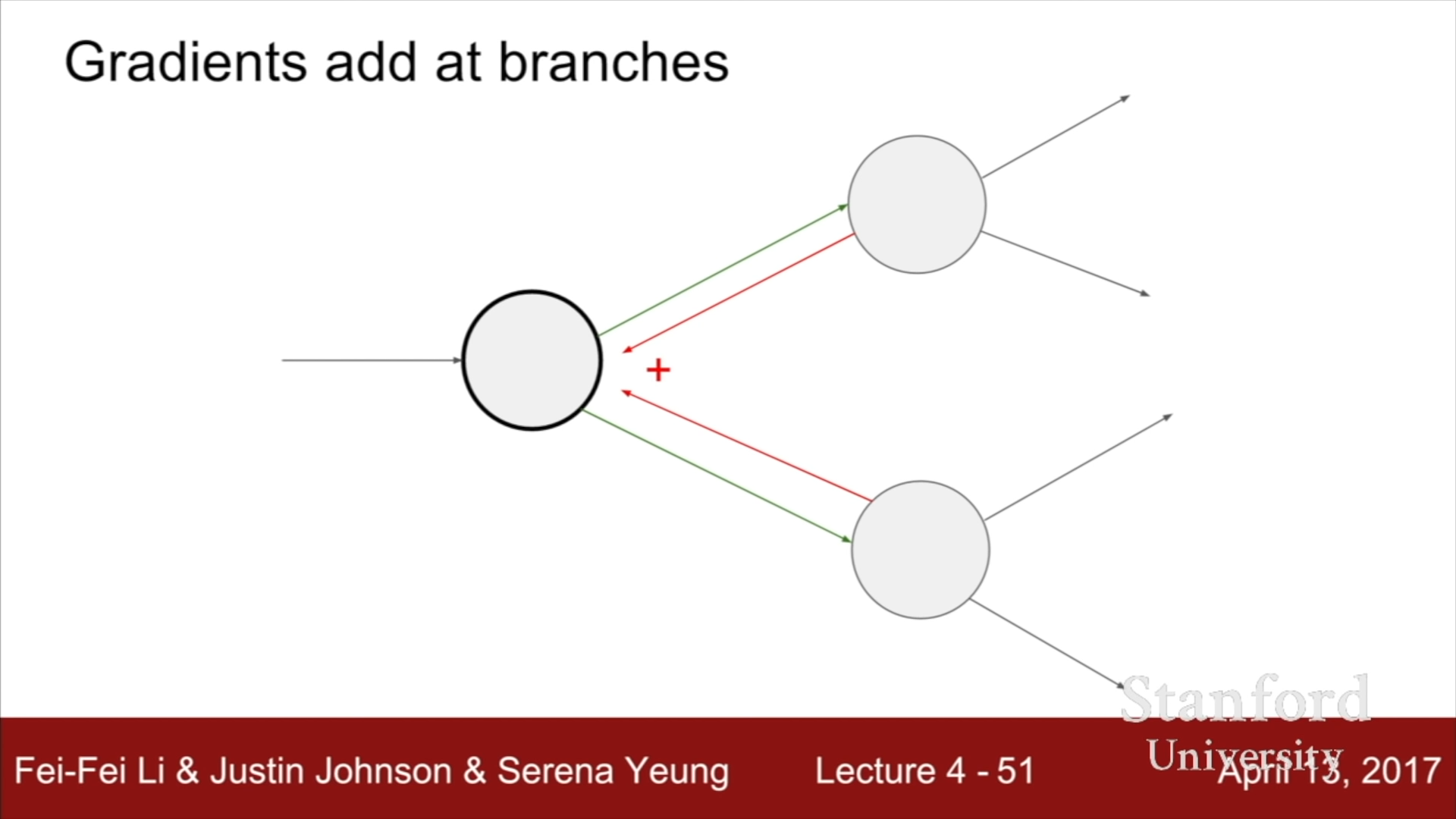
Gradient add at branches

위의 그림에서처럼 Forward의 경우, 하나의 node에 여러개의 node가 연결된 경우, 이전 node값의 변화가 연결된 여러 node에 영향을 미치는 것처럼 Backpropagation에선 상위 layer node의 편미분값의 합이 하위 layer node 변수의 편미분 값이 된다.

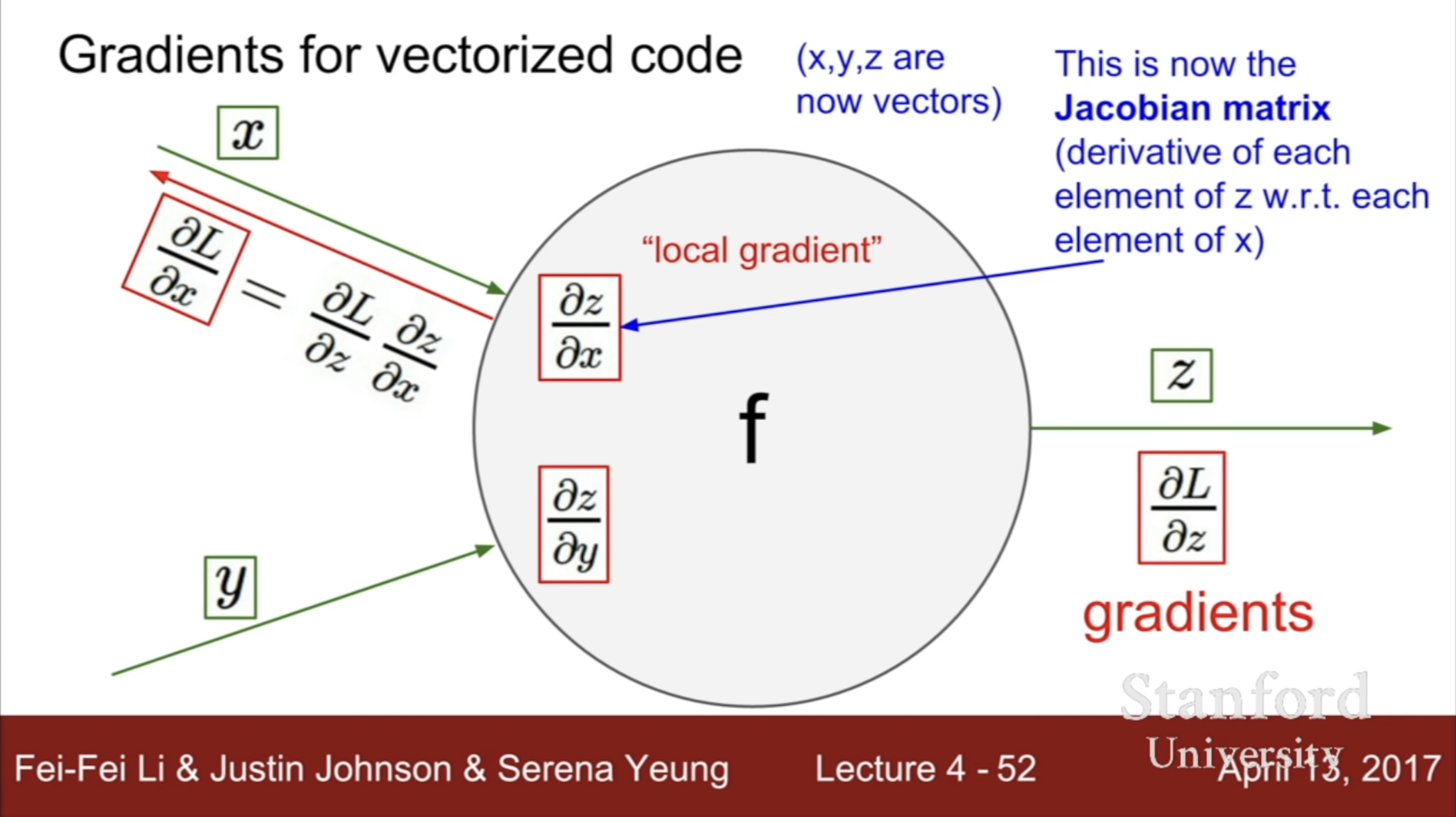
Gradients for vectorized code

만약 input 값이나 output값이 일반적인 변수가 아닌 matrix 형태라면 어떻게 될까?

백터의 편미분과 관련한 내용이 제대로 이해되지 않아 추후에 다시 공부할 예정이다.

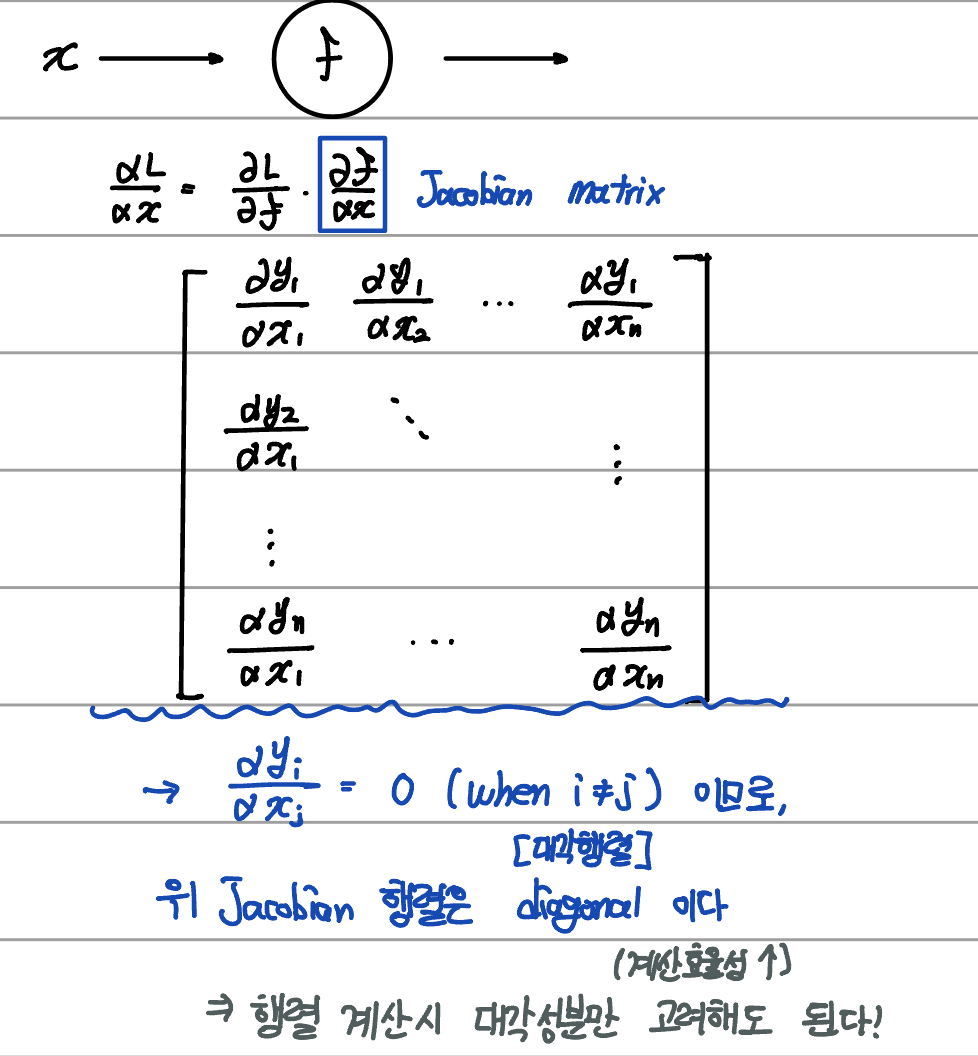
이와 관련한 연산은 Jacobian matrix이다.

위의 사진에서와 같이 x와 y가 각각 matrix인 경우에 하위 layer에 대한 gradient 값은 상위 layer의 gradient에 Jacobian matrix를 곱해준 값이 된다.

아래는 행렬의 편미분(Jacobian matrix)에 관한 내용이다.

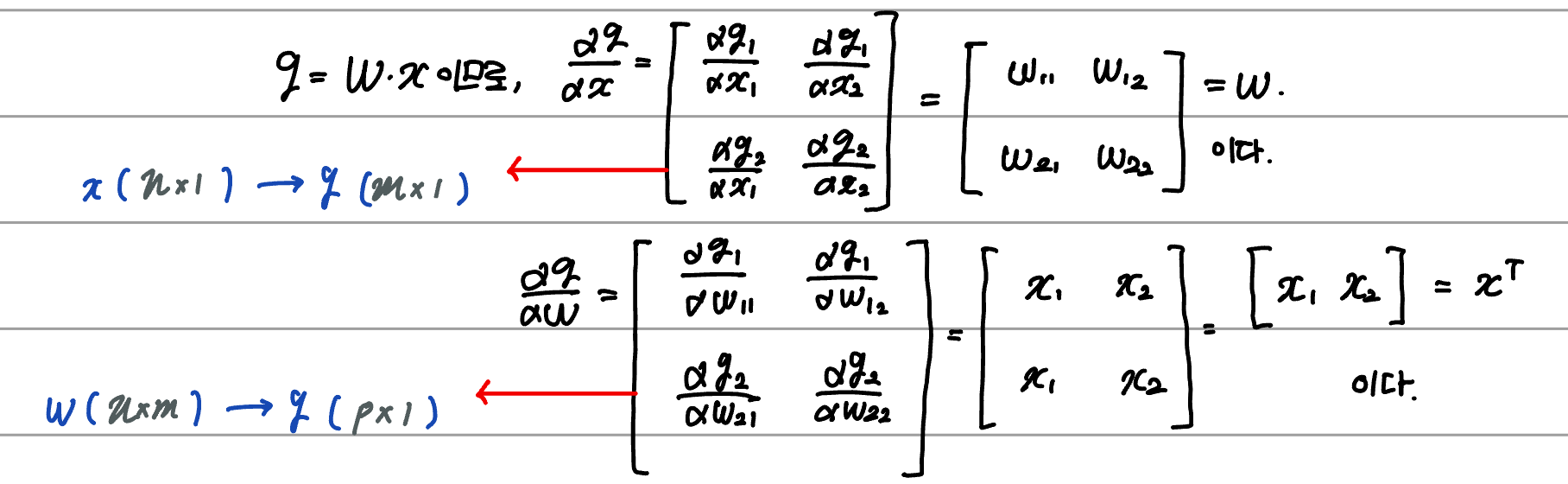
이를 Backpropagation의 편미분 연쇄법칙에 적용할 수 있다.

아래의 예시를 통해 확인해보자.

최종 편미분 값은 원래 행렬의 크기와 동일해야 한다.

Modularized Implementation : Forward/Backward API

Computational Graph를 구현하는 의사코드는 아래와 같다.

        
      
class ComputationalGraph(object):
    #...
    def forward(inputs):
        #1. input gate에 input값을 전달함 (Gradient 연산에 필요한 값을 저장함)
        #2. computational graph를 따라서 진행함.
        for gate in self.graph.nodes_topologically_sorted():
            gate.forward()	
        return loss	# final gate의 output값
    def backward():
        for gate in reversed(self.graph.nodes_topologically_sorted()):
            gate.backward()
        return inputs_gradients	#각 variable의 gradient값을 return함

z = x+y의 덧셈 gate를 구현하는 예시를 살펴보자

        
      
class MultiplyGate(object):
    def forward(x,y):
        z = x*y
        self.x = x	# forward 과정에서 변수의 값을 저장해두어야 한다.
        self.y = y	# backward 과정에서 다시 한번 사용되기 때문이다. 
        return z
    def backward(dz):
        dx = self.y * dz
        dy = self.x * dz
        return [dx, dy]

Caffe Layers와 같은 복잡한 Deep Learning Framework인 경우에도, 소스 코드에서는 Forward와 Backward 식을 포함한 코드를 기반으로 모듈을 형성한 뒤, 이를 적절히 연결하여 여러 복잡한 Layer을 형성한다.

아래는 Caffee Sigmoid Layer이다.

        
      
#include <cmath>
#include <vector>

#include "caffe/layers/sigmoid_layer.hpp"

#ifdef _OPENMP
#include <omp.h>
#endif

namespace caffe {
// 아래는 Sigmoid function의 연산 딘위인 1/(1+e^(-x))의 Forward 연산이다.
template <typename Dtype>
inline Dtype sigmoid(Dtype x) {
  return 1. / (1. + exp(-x));
}

template <typename Dtype>
void SigmoidLayer<Dtype>::Forward_cpu(const vector<Blob<Dtype>*>& bottom,
    const vector<Blob<Dtype>*>& top) {
  const Dtype* bottom_data = bottom[0]->cpu_data();
  Dtype* top_data = top[0]->mutable_cpu_data();
  const int count = bottom[0]->count();
#ifdef _OPENMP
  #pragma omp parallel for
#endif
  for (int i = 0; i < count; ++i) {
    top_data[i] = sigmoid(bottom_data[i]);
  }
}
// 아래는 Sigmoid function의 연산 딘위인 1/(1+e^(-x))의 Backward 연산이다.
template <typename Dtype>
void SigmoidLayer<Dtype>::Backward_cpu(const vector<Blob<Dtype>*>& top,
    const vector<bool>& propagate_down,
    const vector<Blob<Dtype>*>& bottom) {
  if (propagate_down[0]) {
    const Dtype* top_data = top[0]->cpu_data();
    const Dtype* top_diff = top[0]->cpu_diff();
    Dtype* bottom_diff = bottom[0]->mutable_cpu_diff();
    const int count = bottom[0]->count();
#ifdef _OPENMP
    #pragma omp parallel for
#endif
    for (int i = 0; i < count; ++i) {
      const Dtype sigmoid_x = top_data[i];
      bottom_diff[i] = top_diff[i] * sigmoid_x * (1. - sigmoid_x);
    }
  }
}

#ifdef CPU_ONLY
STUB_GPU(SigmoidLayer);
#endif

INSTANTIATE_CLASS(SigmoidLayer);

}  // namespace caffe

Neural Network

이전까지 살펴본 Neural Network 기초는 Linear score function (f = Wx) 이었다. 이 함수에 Non-linear function을 추가하여 2-Layer Neural Network을 형성할 수 있는데, 이는 단순한 Linear function을 이용하여 복잡한 기능을 구현하는 데에 사용될 수 있다.

2-Layer Neural Network에서 주의할 점은 Linear function들 사이에 반드시 Non-Linear function을 사용해야 한다는 것이다. 위의 식에서는 Non-Linear function에 해당하는 max function을 사용했다. 하지만, 반대로 Linear function을 사용한다면, f = Wx 형태의 1차 Linear function에 해당하는 함수로 표현될 것이다. 따라서 **Non-Linear function을 사용해야지만 다층 Linear function을 형성할 수 있다. **

기존의 Linear Function을 생각해본다면 이미지 data x에 대한 각 Class 별 점수를 나타낸 행렬이 h 행렬이었다. 기존에는 W1에 각 Class에 대응되는 template가 한 가지만 존재했었다. 예를 들어 자동차의 template은 왼쪽 아래 사진처럼 빨간색 물체 하나만이 template가 될 수 있었다.

2-Layer Neural Network에서는 반면에, 하나의 Class를 여러개의 형태로 분할할 수 있다. 자동차라고 해서 동일한 색상이나 종류의 자동차만이 존재하는 것이 아니듯이, 빨간 차, 노란 차 등등 여러 개의 Class로 분할하여 각각의 세부적인 template를 형성한다. 이후 형성된 h score과 W2를 이용하여 분류하고자 했던 Class들의 최종 score S를 계산한다. 이는 W2를 이용한 Weighted sum을 이용하여 진행된다.

더 자세히 살펴보면, W1에서 빨간 자동차와 노란 자동차에 대한 Template이 존재하고, 실제 Image data가 빨간 자동차 일때, 빨간 자동차의 score은 높고 노란색 자동차의 score은 낮게 측정이 되어 h의 행렬에 저장될 것이다. 이를 이용하여 계산한다면, W2의 weighted sum을 거쳐 자동차에 대한 점수는 높게 측정이 될 것이다.

이와 같이 Non-Linear function을 이용하여 linear function을 여러 개 중첩한다면, 2-layer뿐만 아니라 여러 개의 다층 구조를 만들어 낼 수 있게 되고, 이를 응용하면 Deep Neural Network를 설계할 수 있다.

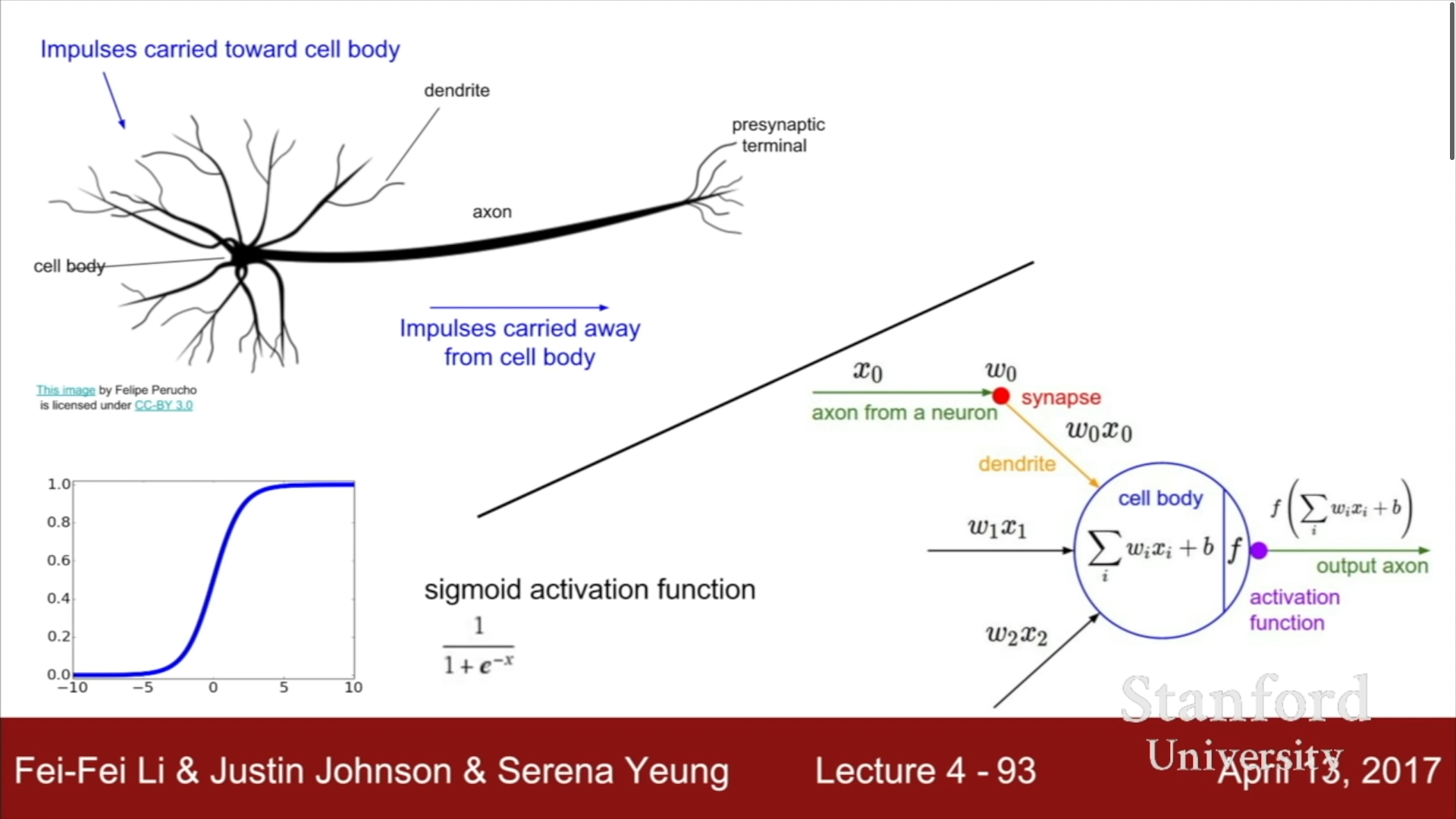
Neural Network & Activation function

신경세포의 작동 방식과 유사하게 Neural Network을 설계할 수 있다. 물론 작동 방식이 아주 유사하지는 않지만, 이전 layer의 신호를 받아 가중치를 곱한 결과를 전부 더해 이를 Activation function에 입력 값으로 사용하고 출력값을 다음 layer의 입력 신호로 활용하는 이 방식은 신경세포와 유사하다.

아래는 Non-Linear한 Activation function의 예시이다.

이중에서 가장 실제 뉴런과 유사하다고 평가받는 함수는 ReLU 함수이다.

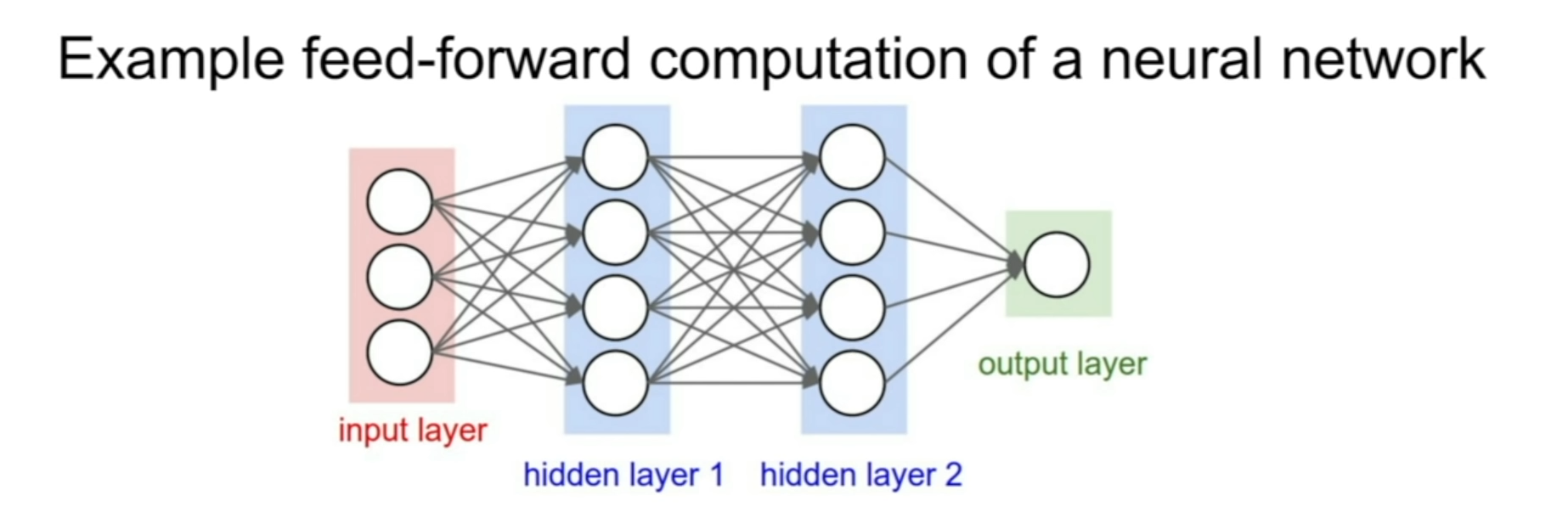
3계층 신경망을 간단히 코드로 나타내면 다음과 같다.

        
      
import numpy as np
import random
f = lambda x: 1.0/(1.0+np.exp(-x))	#Activation function으로 사용할 함수
x = np.random.randn(3,1)	# 랜덤으로 3x1 벡터 생성
h1 = f(np.dot(W1,x) + b1)	# first hidden layer 형성
h2 = f(np.dot(W2,h1) + b2)	# second hidden layer 형성
out = np.dot(W3,h2) + b3	# final layer 형성

다음 강의에서는 Activation function과 CNN에 대해서 공부할 예정이다.

CS231n - Lecture 4

#4 - Introduction to Neural Networks

Further Reading

CS231n - Lecture 1

CS231n - Lecture 2

CS231n - Lecture 3