CS231n - Lecture 5

History of Neural Network

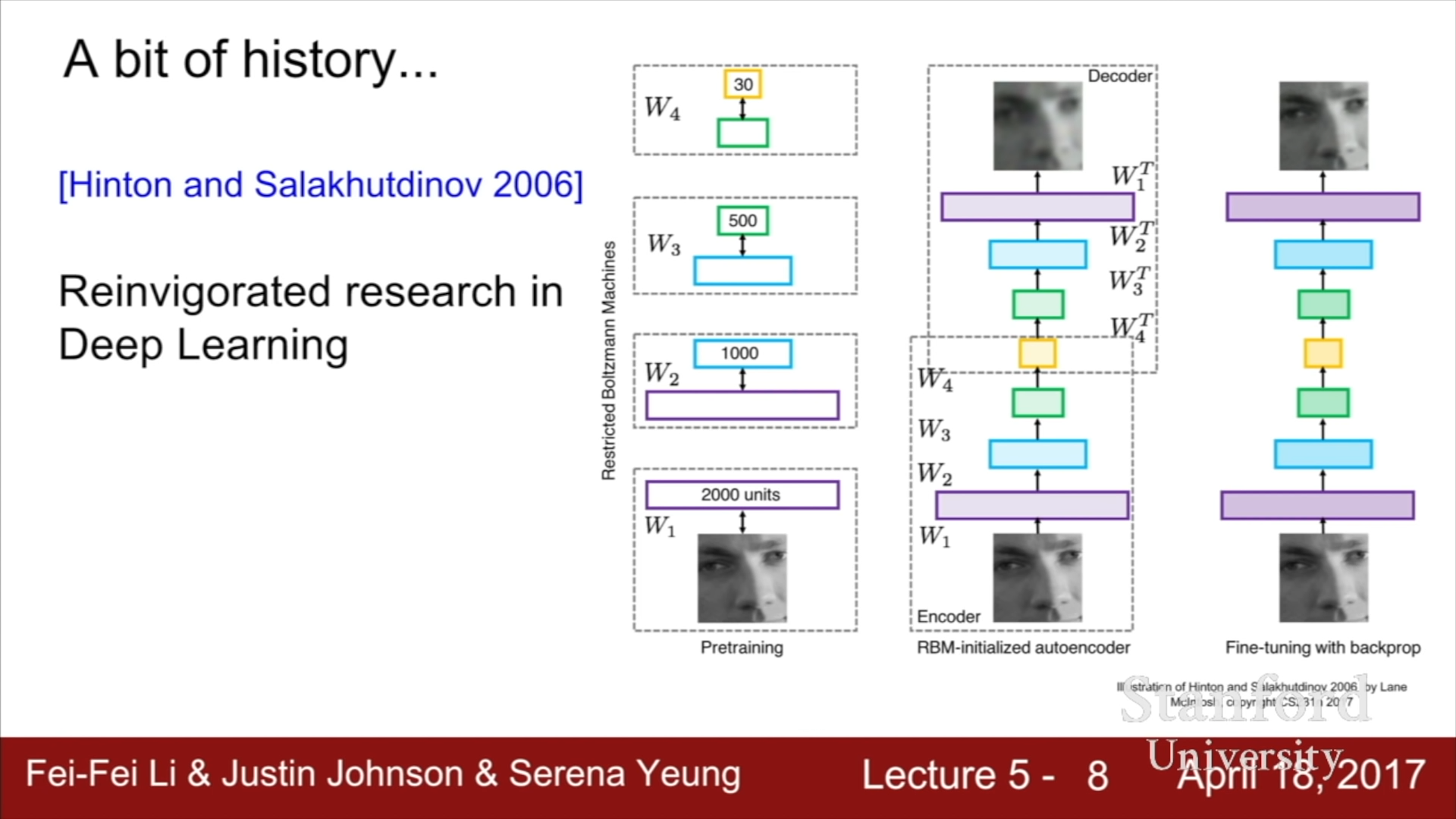
2006년에 Hinton과 Salakhutdinov의 Deep Neural Network를 효과적으로 훈련시킬 수 있다는 논문을 통해 다시 Deep Neural Network에 대한 연구가 활발히 진행되게 되었다. 이 연구는 현대의 Neural Network의 반복과는 상당한 차이가 있지만, Restricted Boltzmann Machine을 통해 각 Layer을 학습시키면서 초기치를 확보하고, 은닉층에 대한 초기치를 전부 확보한 뒤에, 이를 이용하여 전체 Neural Network를 초기화하고, Backprop이나 Tuning을 진행하는 방식이었다.

Neural Network가 인공지능 분야에서 좋은 성능을 보인다는 것은 Acoustic Modeling using Deep Belief Networks 연구에서 Speech Recognition을 성공적으로 마치면서 알려지게 되었고, 이후 ImageNet Classification with Deep Convolutional Neural Networks 연구에서 이미지 분류 분야에서도 뛰어난 성능을 보인다는 점이 입증되었다. 현재는NN의 뛰어난 성능으로 인해 굉장히 다양한 분야에서 사용되고 있다.

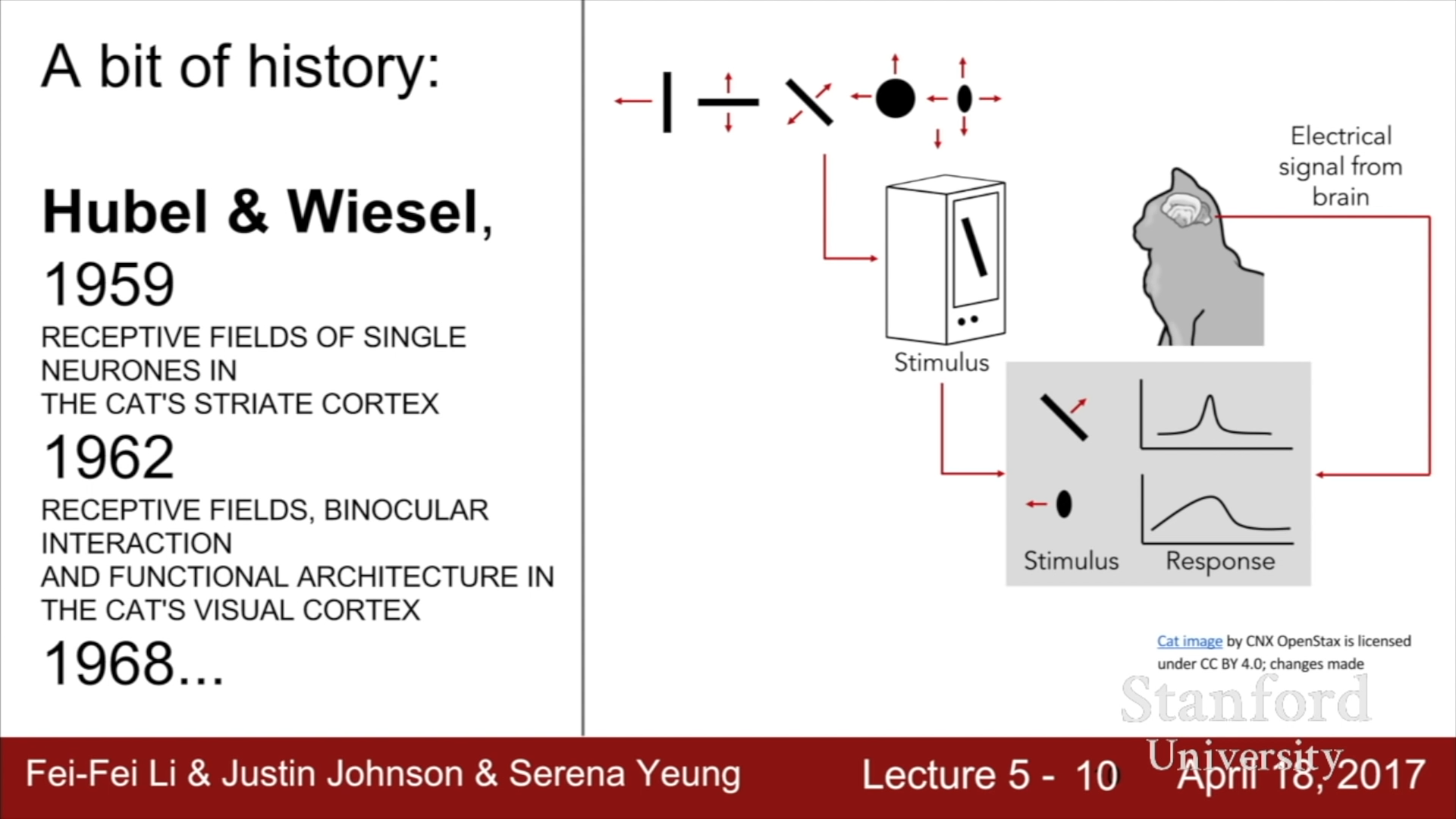
이전 강의에서 다루었던 Hubel과 Wiesel의 고양이를 활용한 Visual Cortex의 작동 방식에 대한 연구를 살펴보면, Visual neurons들이 위계적인 계층구조를 이루고 있다는 점이 밝혀졌다.

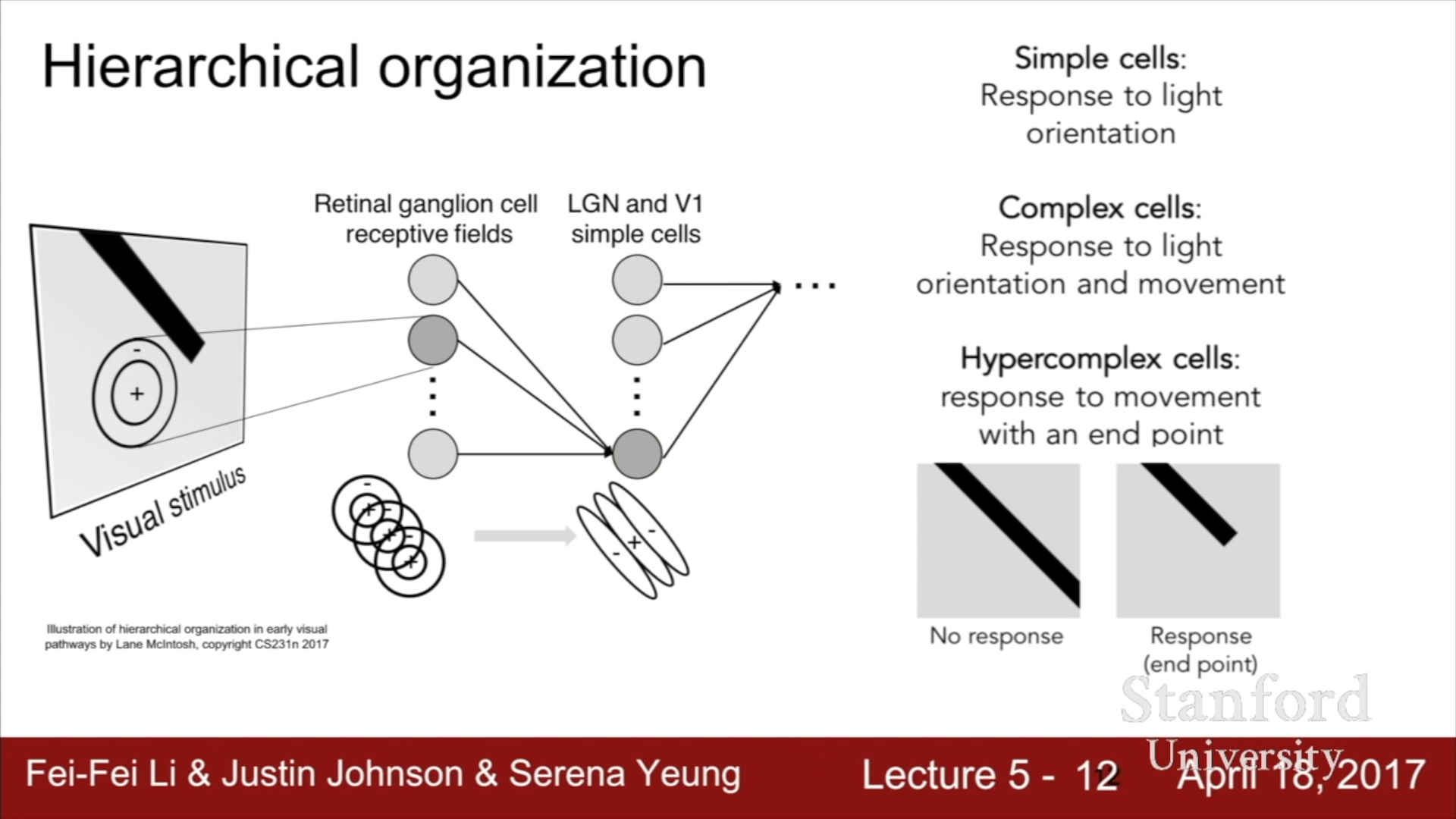
가장 하위 계층인 Retinal ganglion cell에서는 기초적인 원형 형태를 인식하고 점점 상위 구조로 진행할수록 Light orientation, movement, endpoint 등등의 더 복잡한 인식을 수행하는 것이 밝혀졌다. 이 구조를 활용하여 1980년에 Neurocognition에서는 간단한 기능을 수행하는 하위 layer에서 점점 더 복잡한 기능을 수행하는 상위 layer 구조를 개발하였다.

이후에 Gradient based Learning applied to document recognition 연구에서는 최초로 Backpropagation과 gradient based learning을 적용한 모델을 이용한 학습을 진행해 Document recognition에서 좋은 성능을 보여 Zip code Recognition에 꽤 오랜 시간 동안 사용되었다.

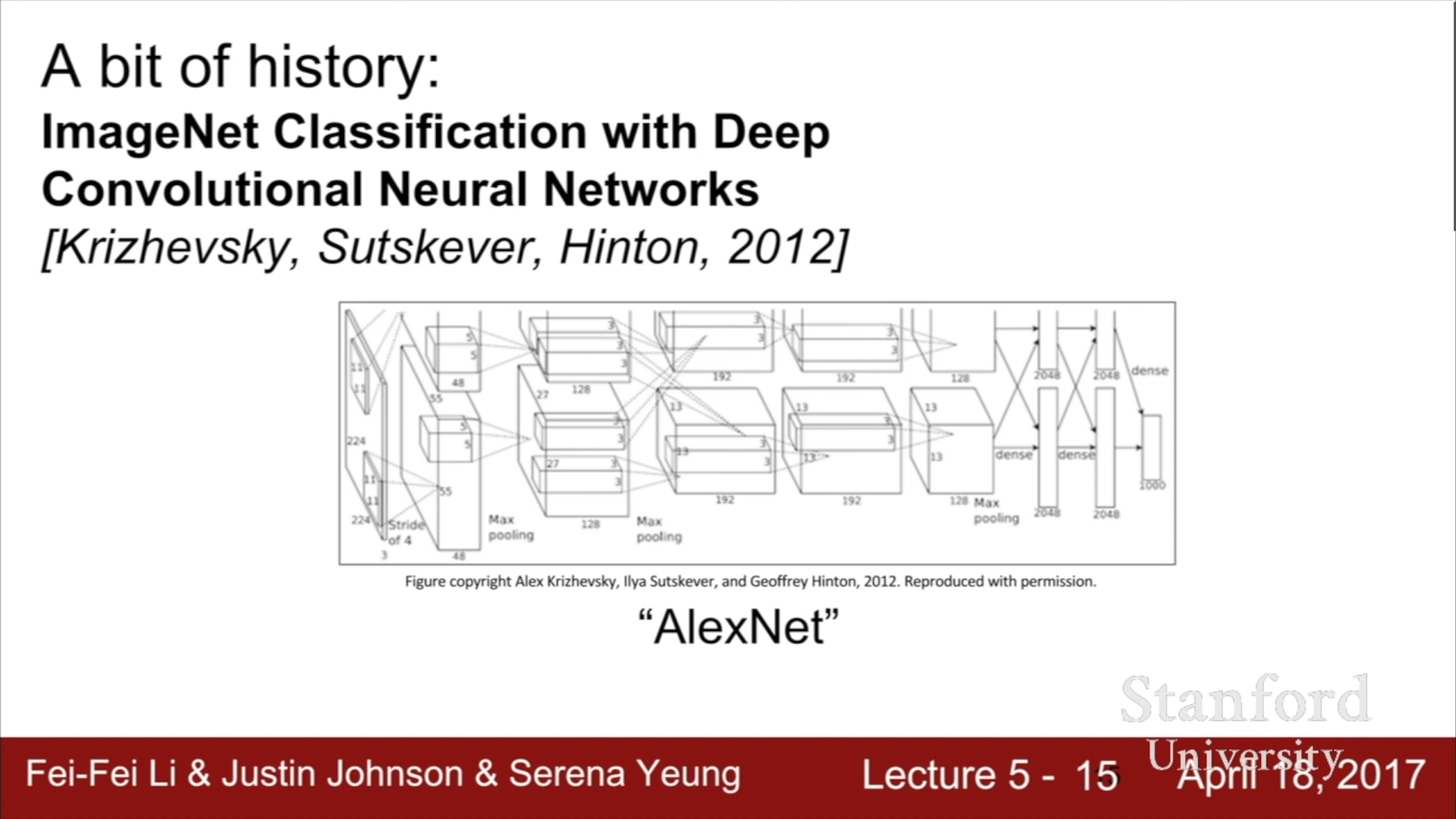
이후 2012년에 ImageNet Classification에서 우리가 현재 사용하는 CNN의 기반 모델의 시초가 되는 AlexNet이 처음으로 소개되었고, 이 구조는 ImageNet data set과 같은 방대한 양의 Image data들과 병렬 컴퓨팅이 가능한 고성능 GPU가 개발됨에 따라서 더 좋은 성능을 가지게 되었다.

ConvNet 기술은 현재 가장 좋은 성능을 보이는 모델로써, Image Classification뿐만 아니라 이미지의 어느 부분이 어떤 것을 의미하는지 찾아주는 Image Detection 기술과 Image Detection에서 더 나아가 어느 픽셀이 어떤 것을 의미하는 지를 찾는 Image Segmentation기술 또한 개발되고 있다. 인간의 동작 인식, 질병 인식, 물체 인식 등등 여러가지 이미지와 관련한 기술들에 CNN이 널리 활용되고 있다.

Convolutional Neural Network (CNN)

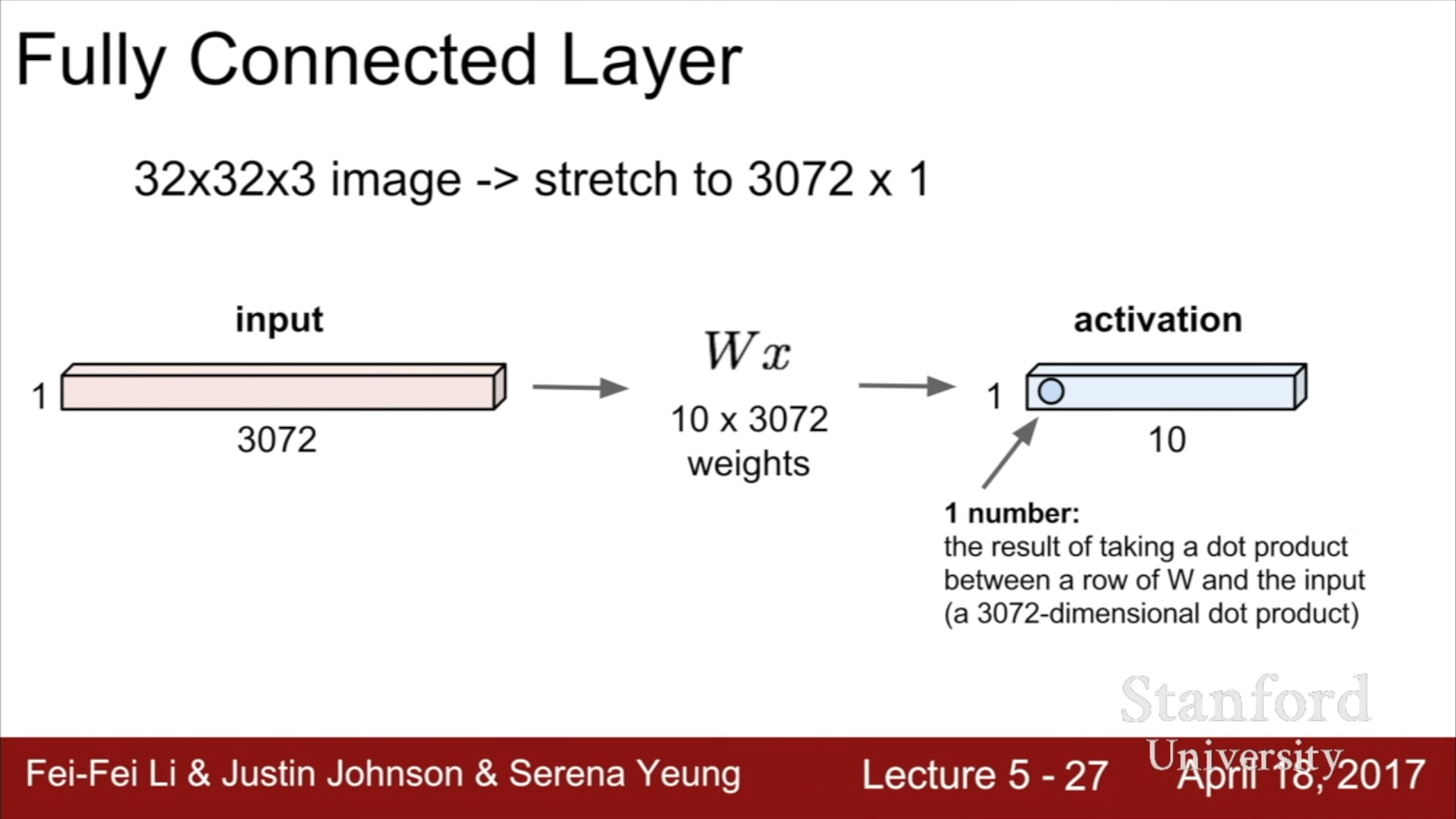
이전까지의 강의에서 다루었던 Fully Connected Layer 를 먼저 살펴보자. 32x32비트 크기의 rgb 정보를 담는 pixel 정보를 이용하기 위해서 32x32x3에 해당하는 3072x1의 Column vector x를 형성하고, 10x3072 크기의 Weights Matrix를 정의하여 Wx의 결과값인 10x1의 Activation map(score)을 생성한다. 이때 10가지의 Score은 각각의 template에 비슷한 정도를 의미하는 척도로 사용된다.

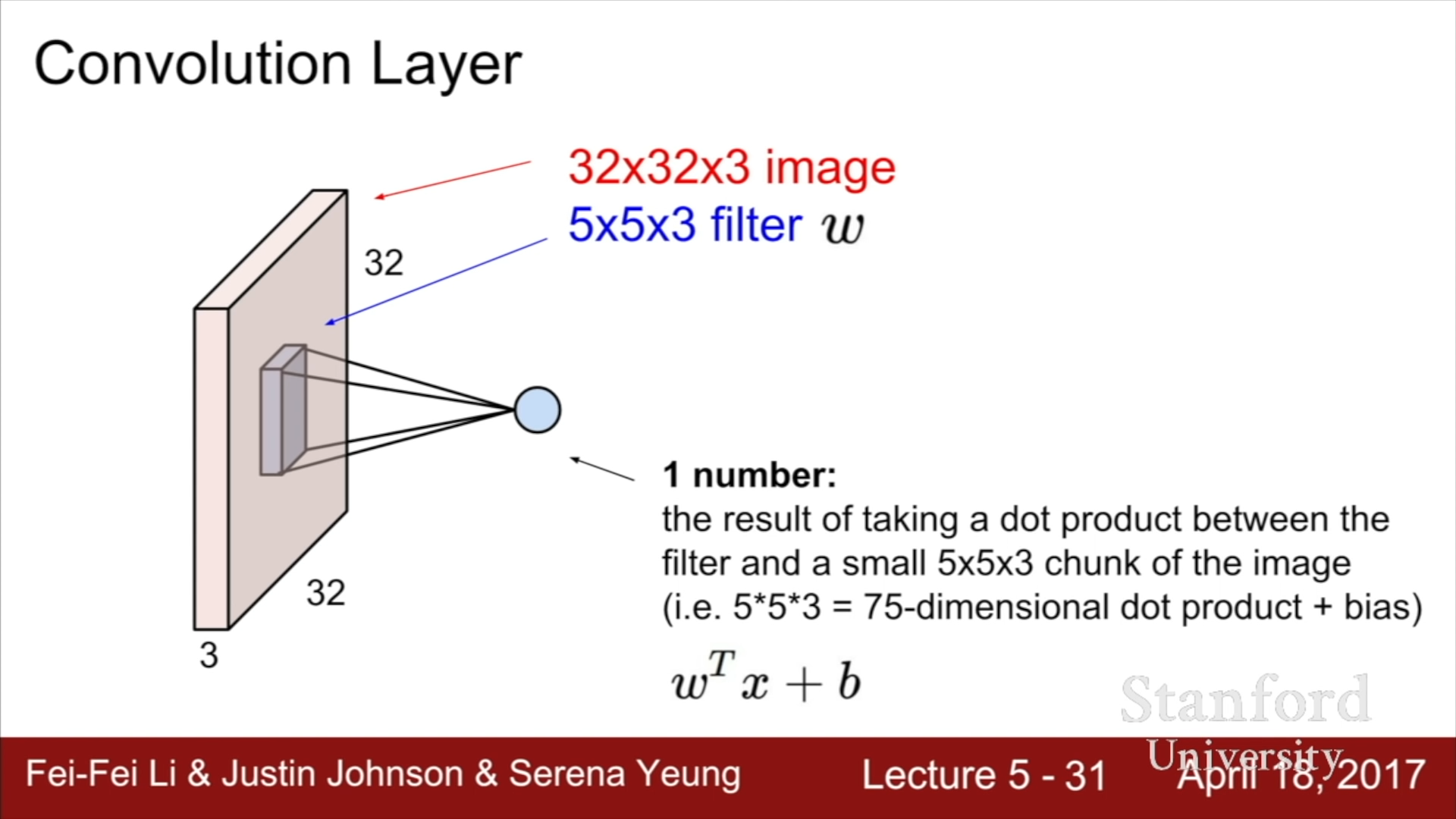
이제 Convolutional Neural Network에 대해서 살펴보자. 먼저 우리가 이전에 살펴 보았던 Fully Connected Layer과의 가장 큰 차이점은 원래 Pixel 정보의 공간적인 구조를 유지한다는 것이다. 아래의 예를 살펴보자면, 32x32x3의 정보를 위의 그림과 달리 하나의 Vector로 간주하지 않고, 공간적인 구조를 유지한 체로 연산을 진행한다.

연산을 위해서 Filter가 필요한데, 이 Filter의 Depth(깊이)는 이전 Layer에 입력된 정보의 Depth와 일치해야 한다.

CNN의 연산은 Input image 와 Filter간의 Dot product로 정의되는데, 위의 예시에서는 5x5x3 짜리의 Image Information Vector와 5x5x3 크기의 Weight Vector 간의 Dot product와 Bias를 더한 하나의 스칼라 값이 연산의 결과가 된다. 따라서 Filter의 parameter 개수는 Weights의 개수와 bias 하나를 더한 값이 된다. 위의 Filter의 경우에는 76개가 된다.

이 연산에서는 Filter를 Image matrix 위에 두고 일정 크기만큼 이동시키며 filter의 각 요소들에 상응하는 Image value들과 filter value의 곱의 합으로 생각할 수 있고, 혹은 해당 Value들과 Filter를 하나의 1x75 크기의 벡터로 형성한 뒤, 두 벡터의 내적을 수행하는 방식으로 생각할 수 있다.

위 연산을 수식으로 표현하면 위의 식과 같다. 이는 Convolution(합성곱)연산에 해당한다.

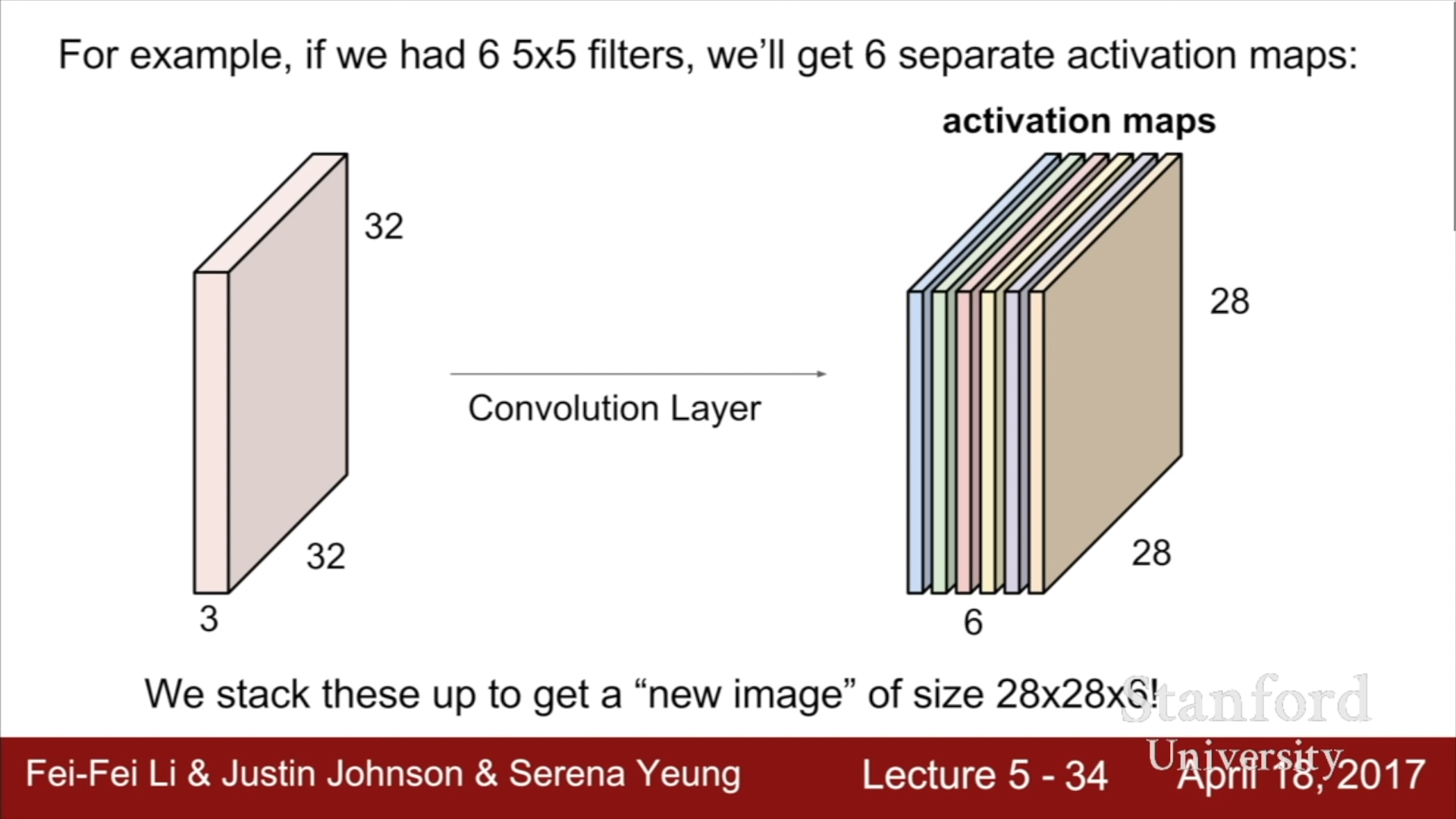
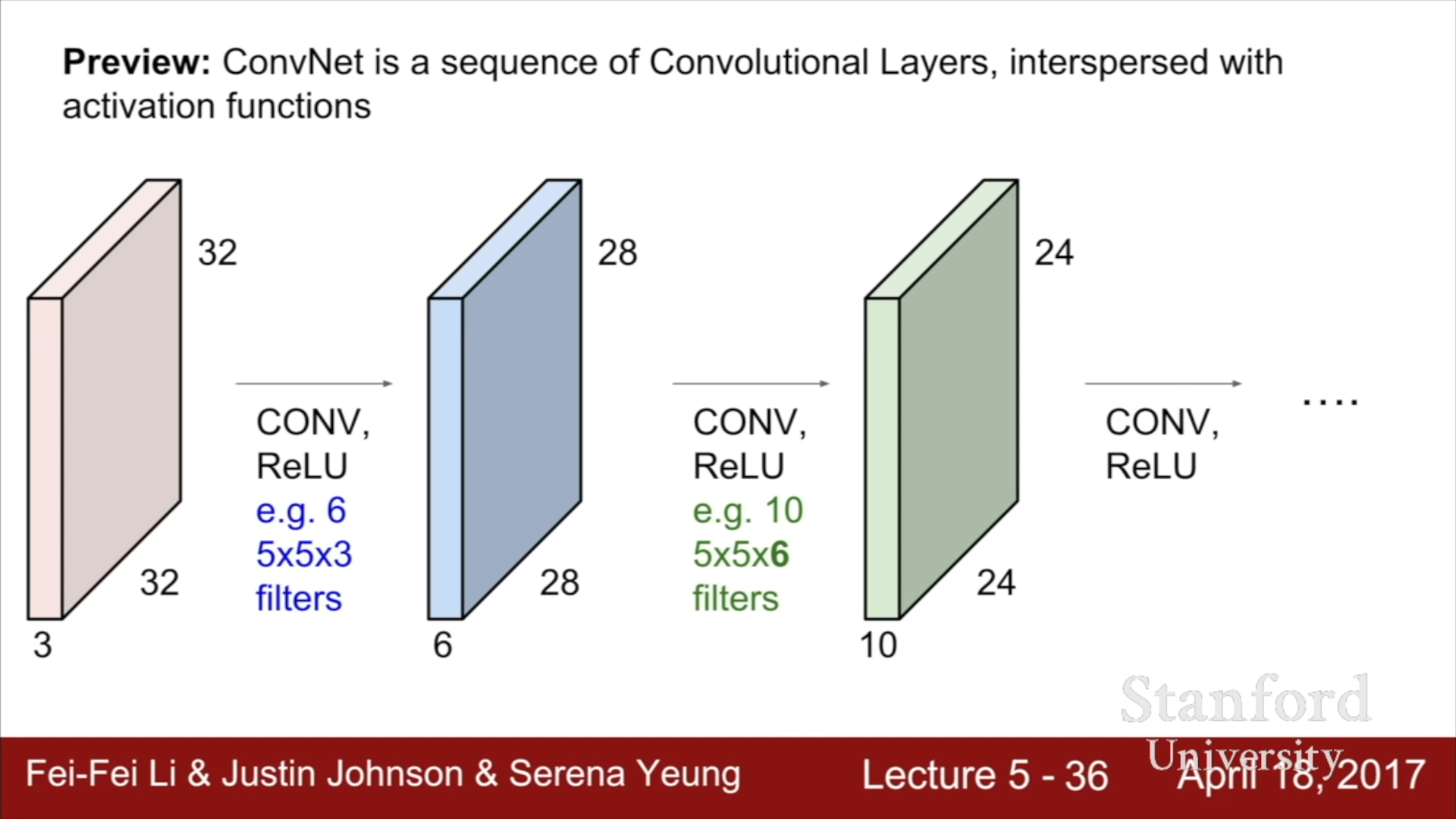
Filter를 옆으로 한 칸씩 이동시키며 연산을 수행해나간다면, (32 - 5 + 1) x (32 - 5 + 1) 크기의 Activation map이 형성된다. 이때, 각 Filter는 어떤 특정한 종류의 Template이나 Concept에 대한 결과를 살펴보는 것이기에 하나의 Filter를 사용하는 것이 아닌 여러 Filter를 사용하게 된다. 만약 6개의 Filter를 사용하게 된다면, 다음 계층의 입력 정보는 6의 Depth를 가지게 될 것이다.

ConvNet은 이런 CONV(Convolutional Layer) 구조와 ReLU와 같은 Activation function이 반복되는 구조로 되어있다.

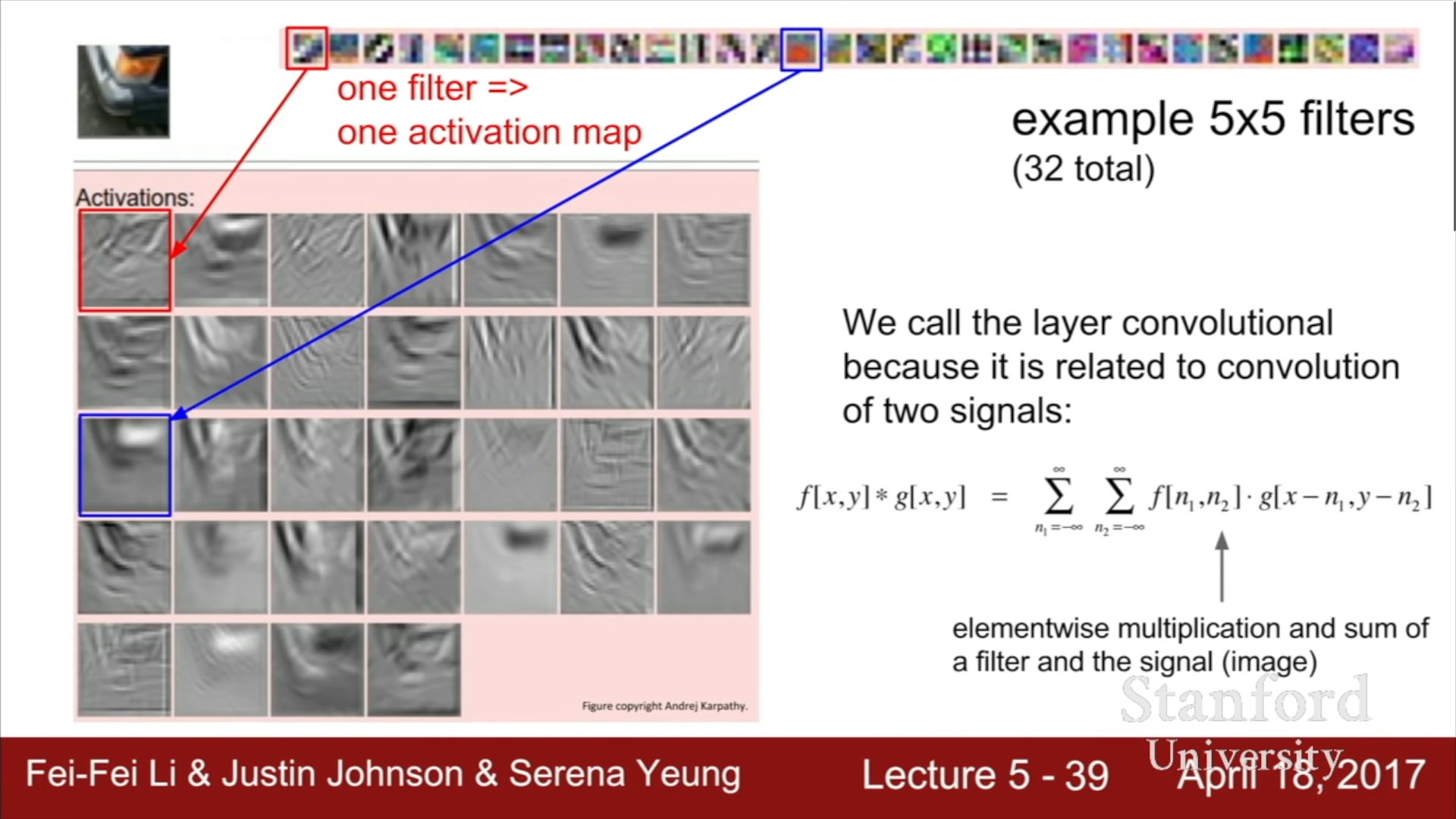
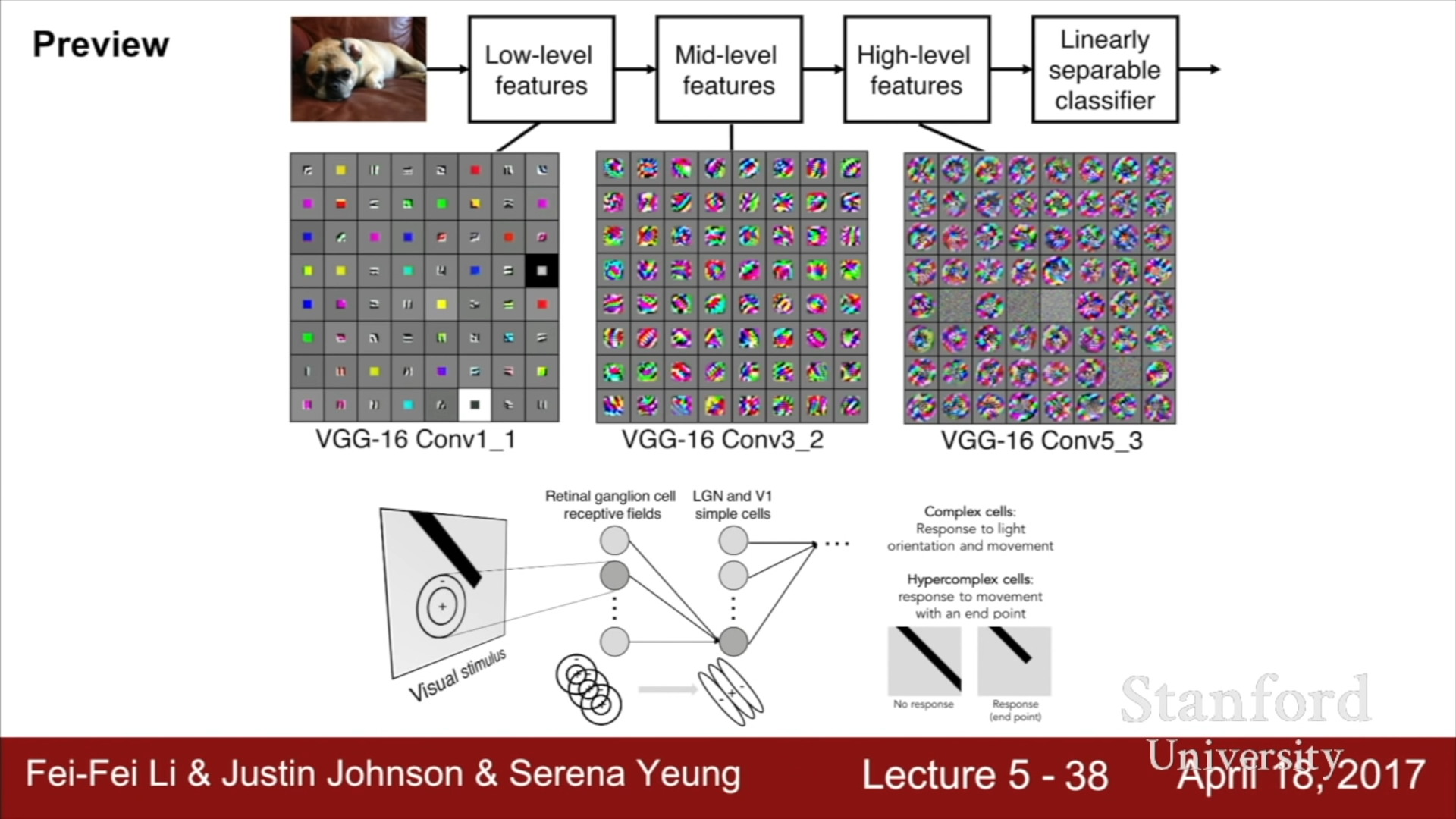
ConvNet 구조를 활용한다면, 하위계층에서는 이미지의 경계와 같은 하위 정보를, 상위 계층에서는 더 복잡한 상위 정보를 담는 구조가 형성되는데, 이는 인간이 의식적으로 이를 강제하지 않았지만 Hubel과 Wiesel의 연구와 매우 유사하다는 점을 파악할 수 있었다.

위 이미지에서 각각의 그리드 속의 그림은 각각의 뉴런이 어떤 상태일 때, 가장 높은 활성도를 보이는 지를 나타낸 것이다.

CNN의 전체 구조

대략적인 ConvNet의 구조는 위와 같다. Convolution Layer와 Non-Linear Layer에 해당하는 ReLU가 몇번 반복되고, Activation map를 Downsampling하는 POOL Layer가 존재한다. (CONV/RENU)^n + POOL 구조가 몇번 반복되고 난 뒤에, 우리가 이전에 살펴보았었던 Fully Connected Layer가 마지막 최종 점수를 구하기 위한 함수로 이용된다.

CONV layer의 spatial dimensions

Convolutional layer에서는 필터를 일정한 크기 만큼 이동시키면서 연산한 값들을 Activation map으로 다음 layer의 input값으로 사용된다. 이때 이동시키는 칸 수를 Stride라고 부른다. 예를 들어 7x7 input을 3x3 크기의 filter을 가지고 stride 1로 Activation map을 형성한다면 5x5 크기의 map이 형성될 것이고, stride 2로 Activation map을 형성한다면, 3x3 크기의 map이 형성될 것이다.

이를 정리하면 위와 같은 공식이 도출된다. N은 이전 input의 크기를, F는 filter의 크기를, stride는 이동시키는 칸 수를 의미한다. (N-F)/Stride의 값이 자연수가 아니라면, map를 제대로 형성할 수 없다는 것을 의미하므로, Stride값은 N-F의 약수들 중 하나여야만 한다.

실제로 CNN 필터를 사용하는 경우, 테두리에 Zero pad를 추가하여 원본 이미지의 Spatial dimension을 최대한 유지시켜줄 수 있다. 7x7 이미지 데이터에 Zero pad를 추가하여 연산을 진행한다면, 3x3의 필터를 이용하는 경우, Activation map의 크기는 (9 - 3)/1 +1로 7x7의 크기를 유지할 수 있게 된다. Zero padding은 원본의 크기를 유지하기 위해 사용하는 하나의 방식일 뿐, 실제로는 여러가지 방법이 사용될 수 있다. 원본의 크기를 어느정도 유지시키지 않는다면, Activation map은 연산을 진행함에 따라 매우 빠른 속도로 크기가 줄어들기에 Edge information과 같은 중요한 정보를 잃지 않기 위해서라면 위와 같은 과정이 필요하다.

위의 예제에서는 간단하게 2차원으로 나타내어 Activation map의 형성 과정을 살펴보았는데, 실제로는 2차원의 Input값이 아니라 3차원의 Input값과 3차원 filter의 내적값을 이용한다는 점을 기억해야 한다.

또한, 실제 CONV Layer에서는 Filter size에 따라서 Zero padding의 두께가 달라진다. Stride가 1인 경우로 예를 들자면, 위에 제시된 공식에 따라서 Activation map의 크기는 (N - F + 1) x (N - F + 1)의 크기를 가지게 될 것이고, Input map과 동일한 크기(N)을 유지하기 위해서라면, Zero padding을 (F - 1) / 2 만큼 붙여주어야 한다. 예를 들면 3이라면 1, 5라면 2, 7이라면 3 두께의 padding을 추가해주어야 한다.

Spatial Convolution Representation with Torch

        
      
module = nn.SpatialConvolution(nInputPlane, nOutputPlane, kW, kH, [dW], [dH])
# nInputPlane = 입력되는 input plane의 개수
# nOutputPlane = 출력되는 output plane의 개수
# kW = kernel(filter)의 너비
# kH = kernel(filter)의 높이
# dW = Stride의 너비 이동수
# dH = Stride의 높이 이동수
# padW = 추가된 세로 Zero padding 수
# padH = 추가된 가로 Zero padding 수

owidth = floor((width + 2*padW - kW)/dW + 1)
oheight = floor((height + 2*padH - kH)/dW + 1)

#input plane : nInputPlane x kW x kH
#output plane: nOutputPlane x owidth x oheight

Convolutional Layer의 input과 output을 Torch 언어로 표현하면 위와 같다.

Brain/Neuron view of CONV Layer

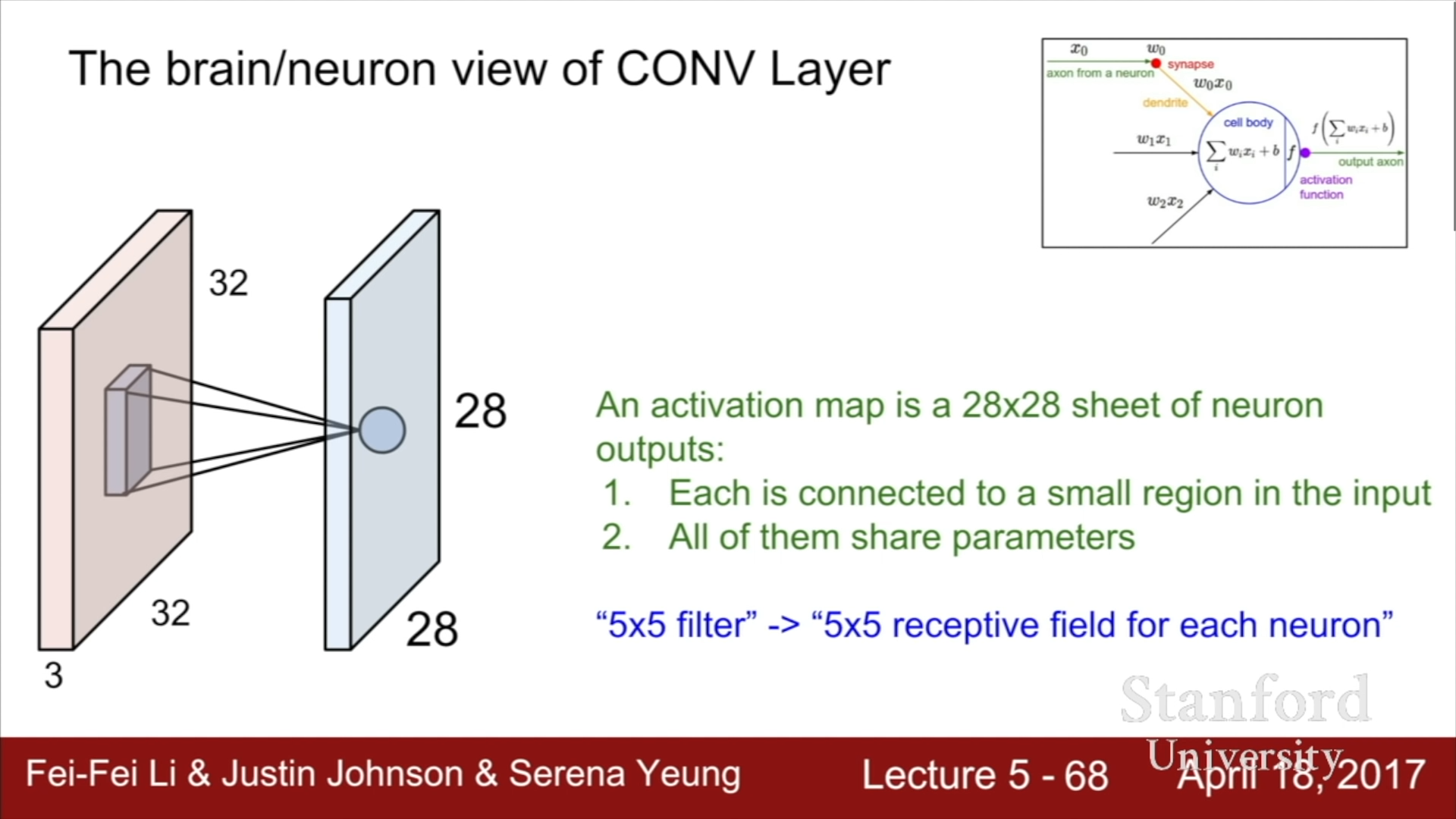
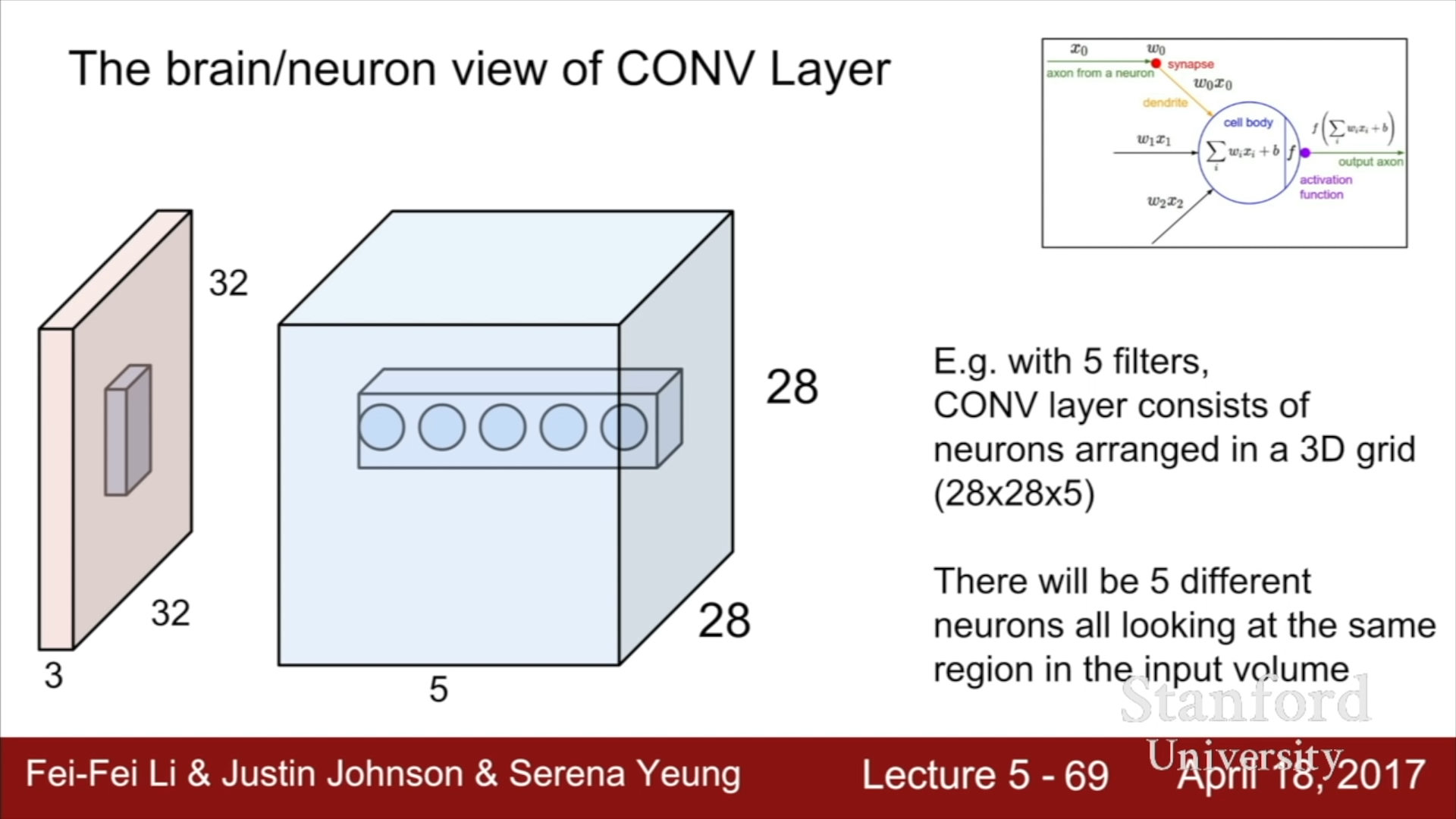
Neuron의 구조는 이전 뉴런의 신호에 가중치를 곱한 값의 합에 bias를 더해 activation function의 input값으로 사용하는데, Convolutional layer는 이를 local하게 바라보고 spatial dimension을 유지시켜주는 것과 동일하다. 즉, 뉴런의 구조는 Fully connected layer과 같이 input값을 global하게 전부 다루는 것이고, Convolutional layer는 필터를 사용하여 전체 Input값이 아닌 Input값들 중 일부를 local하게 바라본다는 것을 의미한다.

Fully Connected Layer의 경우에는 Activation map의 각 value는 전체 input값을 이용하여 도출한 값이지만, Convolutional Layer의 경우에는 Input map의 일부를 이용하여 도출한 값이라는 차이점이 존재한다.

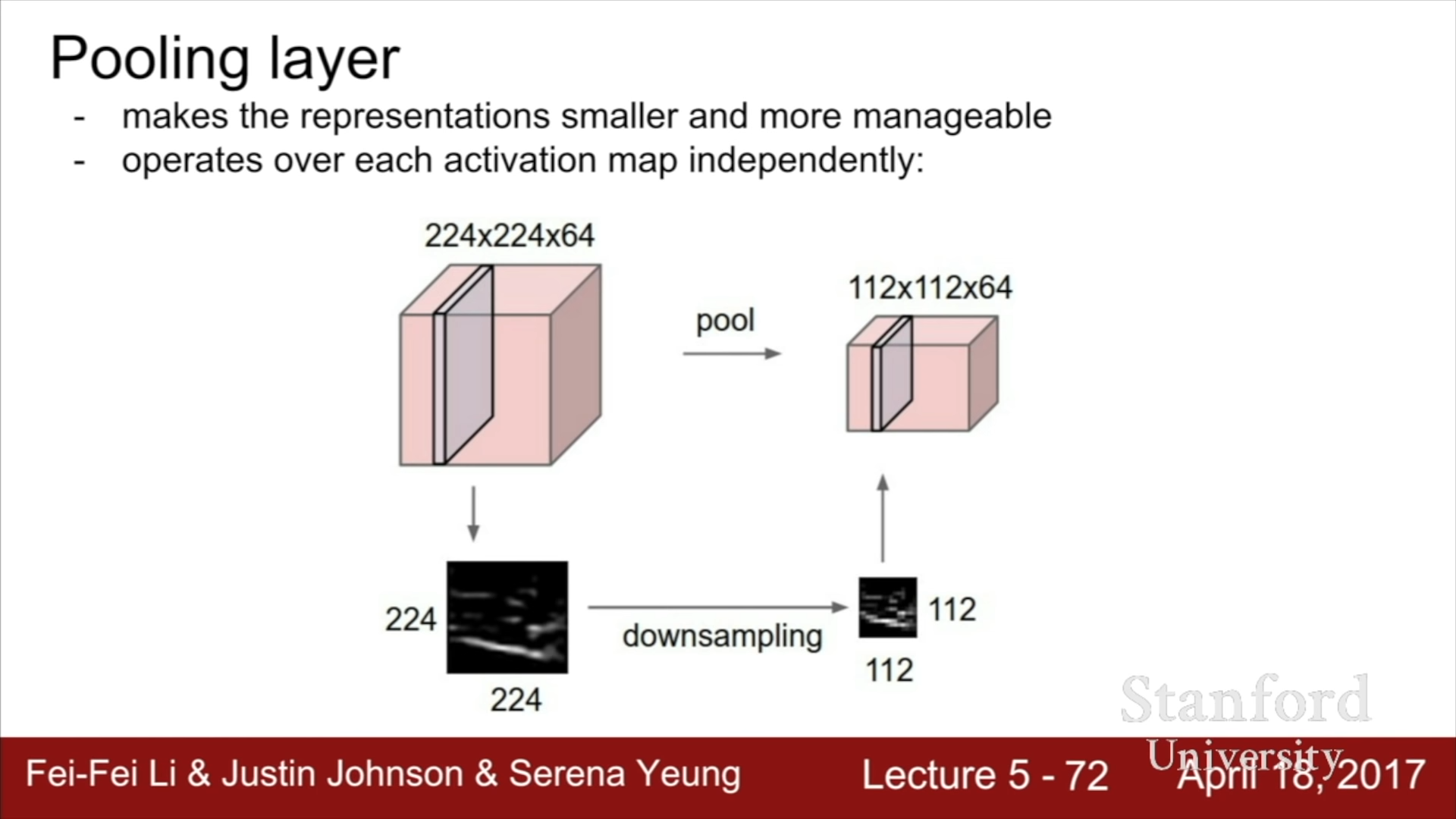
Pooling Layer

Polling layer의 경우에는 Input depth와 Output depth가 동일하고 단지 각 Output map들의 크기만 줄이는 것을 의민한다. 이 과정에서 사용되는 가장 대표적인 방법이 Max Pooling 방식이다. Max pooling 방식은 max를 구하는 2x2 filter를 stride 2를 가지고 연산을 진행하는 방식이다 이렇게 된다면, 너비와 높이를 절반으로 줄일 수 있다.

Q1. Pooling layer로 max pooling이 아니라 Average pooling과 같은 다른 방법을 사용할 수 있지 않는가?

물론 Average pooling 방식을 사용해도 무방하나, 해당 위치에서 얼마나 해당 신경이 반응을 했는지를 판단해주는 문제이기 때문에 Max pooling 방식을 사용하는 편이 더 좋다.

Q2. Stride와 Pooling은 비슷한 DownSampling 효과를 가져다주는데, Pooling layer 대신 Stride를 사용할 수 있는가?

Stride와 Pooling Layer 전부 DownSampling에 사용되고, 최근 연구를 보면 실제로 Pooling 대신 Stride를 사용하기도 한다.

위는 Pooling layer를 이용하여 input의 크기를 줄이는 공식이다. 일반적으론 2x2짜리 필터와 Stride 2, 3x3짜리 필터나 Stride 3의 설정을 사용하여 Pooling을 진행한다.

ConvNet에서의 Fully Connected Layer

Convolutional Neural Network의 output값을 기존의 Fully Connected Layer의 input matrix와 같이 1D 형태의 vector로 변환해주고, 이를 Weight matrix와의 dot product를 통해 최종적인 점수를 구한다. 결국, ConvNet의 중간 과정에는 Spatial structure가 유지되나 마지막 score를 구하는 과정에서는 모든 value들을 통합하여 score를 구하는 데에 사용한다.

ConvNet의 초기 Layer에는 경계, 가장자리와 같은 기본적인 정보를 가진 map(edge map)이 형성되어 다음 input map으로 사용되고, 더 상위 layer로 진행할수록 하위 layer에서 제공한 map를 이용하여 더 복잡한 map(Corner map …)을 형성하게 된다. 따라서 각 layer의 결과값은 찾고자 하는 template이 얼마나 fire되는지를 의미하고, 상위 계층으로 진행할수록 이전단계의 map을 이용하여 더 복잡한 특징을 검출하고 이를 또 다시 map으로 만들어준다.

Summary

최종적인 구조는 위와 같다. (CONV - RELU) 가 N번 진행된 후 POOL을 거치는 과정을 M회 반복한다. 이후 최종적인 score 도출을 위해 Fully Connected layer과 ReLU function을 이용하는 과정을 1에서 2회 반복한다, 이후 SoftMax function을 통해 최종적인 score과 정답이 얼마나 차이가 나는 지를 확인할 수 있게 된다.

CS231n - Lecture 5

#5 - Convolutional Neural Network

Further Reading

CS231n - Lecture 1

CS231n - Lecture 2

CS231n - Lecture 3