Fully Connected Layer / Activation Function
Seq2Seq RNN에 대해서 공부하던 중에 Decoder의 최종 출력값을 정하는 부분에 Fully Connected Layer(Dense Layer)가 쓰이는 것을 확인할 수 있었다. 비단 RNN 뿐만아니라 다른 여러 DNN 프레임워크에서 굉장히 자주 등장하는 Fully Connected Layer이므로 이를 정리하고자 이 포스팅을 작성한다. **
Fully Connected Layer
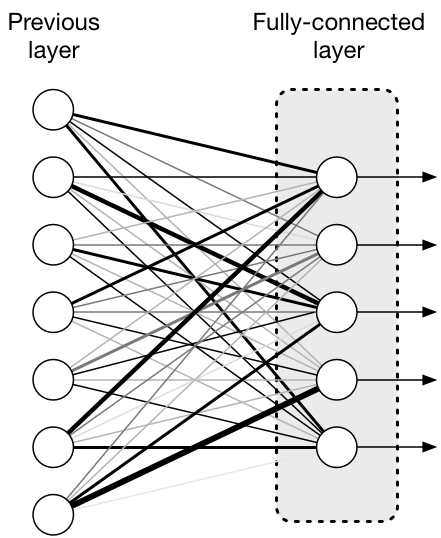
Fully Connected Layer는 우리말로 완전 연결 계층이다. 이 말은 한 층의 모든 뉴런(cell)이 다음 계층의 모든 뉴런과 연결이 된 Layer를 의미한다. 이 Layer는 아래와 같은 그림으로 표현할 수 있다.
위 그림을 참고한다면, Fully connected layer의 모든 뉴런과 이전 layer의 모든 뉴런이 전부 대응되는 것을 확인할 수 있으며, FC Layer의 결과값으로 나오는 것은 1차원 배열 형태로 평탄화되어 있다. 따라서 CNN에서는 이미지 분류를 위한 1차원 배열 평탄화로 사용할 수 있는 것이다. 또한, RNN 중에서 Seq2Seq에서는 token 선택을 위한 1차원 배열 생성에 활용할 수 있다.
결국, Fully Connected Layer는 이전 Layer까지의 학습합 데이터를 가지고 최종적인 선택을 내리는 과정에서 필요한 1차원 배열을 생성하는 평탄화 과정에 필요한 layer이다.
Activation Funciton
Fully Connected Layer와 함께 거의 붙어다니는 것이 바로 Activation Fuction이다. 이는 우리말로 활성화함수라고 불리며, 여러가지 함수가 각 용도에 맞게 쓰이고 있다. 대표적으로 sigmoid, ReLU, tanhx, softmax 함수 등등이 있다.
Activation Function의 경우, 두가지 기능이 존재한다.
비선형성 부여
가장 먼저, 그리고 가장 중요한 기능은 바로 비선형성을 부여한다는 것이다.
아래는 간단한 CNN Layer(ConvNet)를 간단히 표현한 것이다. ConV layer의 중간중간에 ReLU의 활성화 함수를 사용하는 것을 확인할 수 있다. 기본적으로 CNN Layer는 선형적인 구조를 가지고 있다.
f = ax와 g = bx의 함수를 생각해보자. 우리가 더 깊은 네트워크를 생성하는 방법은 layer들을 중첩하는 것이므로, f(g) 둥의 형태로 변환하는 것이다. f(g(x))는 abx 형태이고, ab는 다시 또 다른 상수 c로 표현한다면, f(g(x)) = cx로 표현할 수 있으므로, 복잡한 구조가 아니라 f와 g의 함수와 동일한 복잡도를 가지는 것이다.
동일하게, Tensor끼리의 matmul 연산을 진행하는 과정은 결국, ab의 연산과 동일하므로, 또다른 c의 Tensor로 치환할 수 있기에 선형적인 Layer들을 계속해서 중첩하더라도 성능은 하나의 Layer를 사용하는 것과 동일한 성능을 보일 것이다.
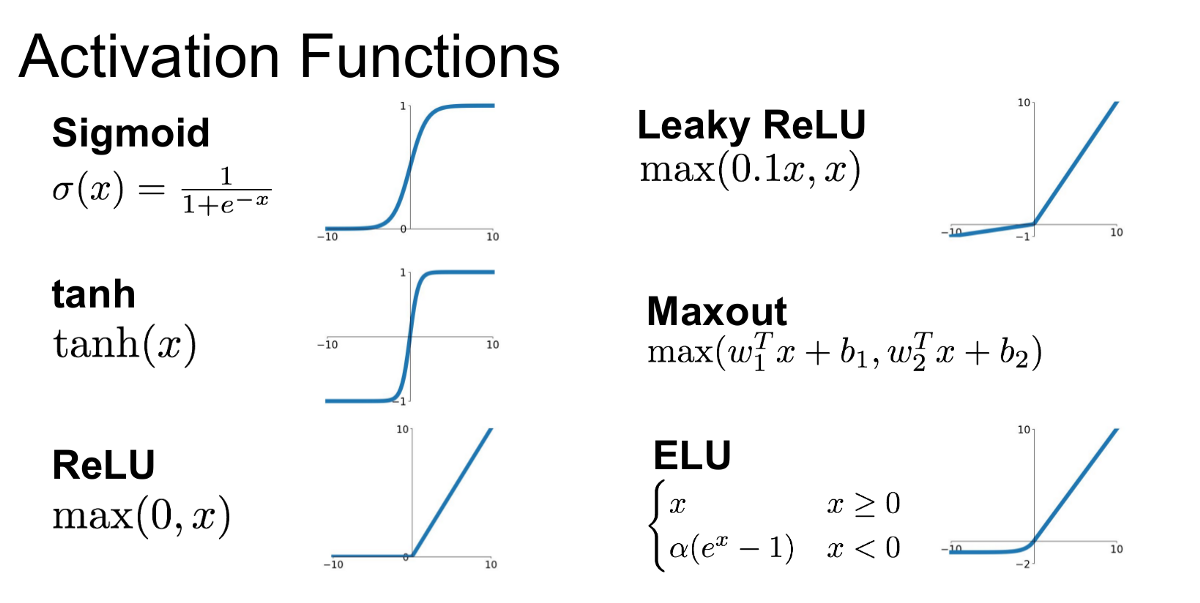
이를 해결하려면, 비선형함수를 선형 Layer들 사이사이에 넣어주어 Collapse 현상을 방지해야 한다는 것이다. 이에 해당하는 것이 Activation Layer들이며 우리가 활성화함수라고 부르는 것들이다. 아래 사진을 보면 그래프가 직선(선형)이 아닌 곡선(비선형) 구조를 보이는 것을 확인할 수 있다.
Activation Function들은 각각 장단점들이 존재한다. 애초에 DNN 설계 과정에서 학습이 가능하려면 미분이 가능해야 하지만, 미분이 쉽지 않은 경우라던지, 혹은 일정 범위를 넘어가면 기울기가 0에 수렴하기에 Vanishing gradient 문제라던지 등등이 존재한다. 그래서 몇몇 Activation Function들은 함수에 중간층(은닉층)에 사용하지 않고 다음 기능에 사용된다.
최종 출력값 선택
예를 들어 위 그림에서 Sigmoid함수를 살펴보자. sigmoid function의 경우, 일정 범위를 넘어가게 된다면 기울기가 거의 0에 가까이 가는 Vanishing Gradient 문제가 발생한다. 이는 특정 기울기 값이 0이 된다면, 그 이후에 역전파되는 기울기 값이 전부 0으로 수렴하므로 효율적인 학습이 불가능해지기에 문제가 되는 것이다.
따라서 다른 Activation Function(ReLU, …)들이 등장함에 따라서 sigmoid function은 중간층에서 거의 쓰이지 않고, 이진분류 문제에서 이 값이 0인지 1인지를 판단하는 최종 출력층에 사용한다.
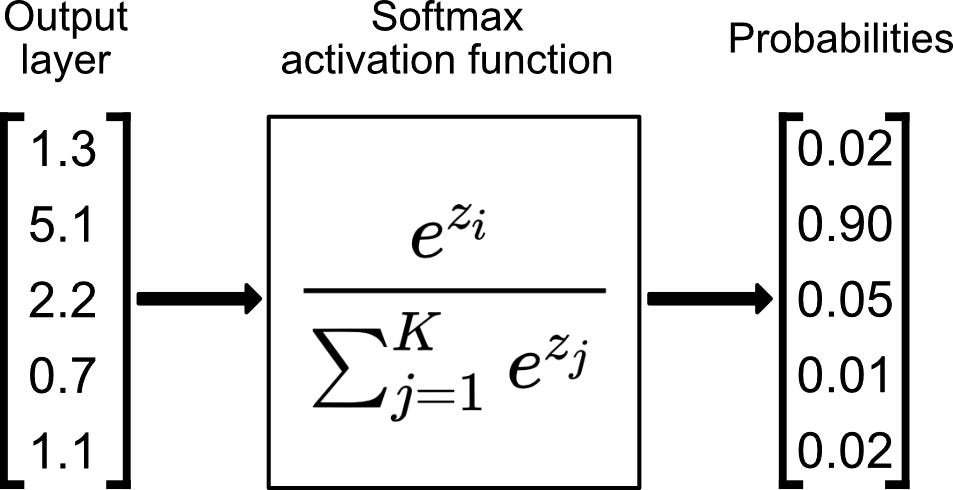
또한, Softmax function의 경우, 다중 분류 문제에서 사용하는 함수로 공식은 아래와 같다.
위 그림에서 Output Layer가 FC Layer를 지나가서 만들어진 평탄화된 Layer에 해당하는 값이고, softmax function을 지나게 되면, 각 class에 대한 확률값이 위와 같은 공식을 통해서 구해진다.