Generative Models - 2. Autoregressive Models

1. Autoregressive Models

자기회귀 모델은 Explicit Model이면서 동시에 Tractable Model이다. 이는 확률 분포를 직접 나타내고, 확률을 직접 계산하는 것이 가능하다는 의미이다. 흔히 자주 쓰이는 Transformer나 RNN 계열 모델들이 모두 이 자기회귀 구조를 가지고 있다.

Next Token Prediction 문제와 같이 다음 Token을 구할 때 이전까지 생성한 모든 Token을 전부 활용하는 것처럼 i번째 output에 대한 확률 분포는 아래와 같이 정리할 수 있다. \(p_\theta(x_i\mid x_1,\dots,x_{i-1})\) 따라서 생성된 모든 $x_1, … x_n$ (x)에 대한 확률값은 아래와 같이 확률 값들의 곱으로 표현한다. \(p_\theta(x_1,\dots,x_n) =\prod_{i=1}^n p_\theta\!\left(x_i \mid x_{<i}\right), \quad x_{<i}=(x_1,\dots,x_{i-1}).\) 이는 Transformer의 근간이 되는 만큼 강력하지만 연산량이 굉장히 크다는 단점이 있다.

2. Parametric Neural Networks

신경망을 설계하는 과정에서 Parameter의 수는 매우 중요하다. 이론적으로 계산이 불가능한 만큼의 파라미터 수를 가진다면 해당 신경망은 쉽게 사용할 수 없을 것이다. 어떤 data $D = [x_1, x_2, x_3, x_4]$의 확률값 $p_{\theta}(x_1, x_2, x_3, x_4)$를 구하는 과정에서의 파라미터 수를 고려해보자.

2.1 Chain Rule

$x_i$ 각각이 0 또는 1의 값을 가지는 베르누이 확률 분포를 따른다면

• $P(x_1)$의 값을 담는 파라미터 1개
• $P(x_2 \mid x_1)$의 값을 담는 파라미터 2개 ($x_1$의 값이 0인 경우와 1인 경우 저장)
• $P(x_3 \mid x_2, x_1)$의 값을 담는 파라미터 4개 ($x_0, x_1$ 값이 각각 0 또는 1인 경우 저장)

\[p(x_1, x_2, x_3, x_4) = p(x_1)\, p(x_2 \mid x_1)\, p(x_3 \mid x_1, x_2)\, p(x_4 \mid x_1, x_2, x_3)\]

따라서 4개의 데이터를 담는 파라미터의 개수는 최소한 $1 + 2 + 4 + 8 = 15$개의 파라미터가 필요하게 된다. $n$개의 데이터만큼의 Joint distribution을 구하기 위해서는 따라서 $2^n - 1$개 만큼의 파라미터 개수가 필요하고 $O(2^n)$의 파라미터가 요구된다.

위 가정은 아무런 제약도 가하지 않은 상태로 모든 값을 저장한다고 가정했을 때의 문제이다. 추가적으로 위 가정이 이진 분류 가정이 아닌 더 많은 k Category분류라고 하면 $k^n$에 비례하는 파라미터가 필요하게 된다.

2.2 Bayes Network

연쇄 법칙만을 사용하는 것이 너무나 많은 파라미터를 필요로 하므로, Reinforcement Learning에서 주로 사용하는 Conditional Independence Assumption 조건부 독립 가정을 들고 올 수 있다.

Conditional Independence Assumption은 Current State가 이전의 모든 state의 정보를 담고 있다는 가정으로, 수식으로는 $P(X_i \mid X_{i - 1} = P(X_i \mid X_{i - 1} … X_1)$로 생각이 가능하다는 의미이다.

\[p(x_1, x_2, x_3, x_4) \approx p_{\text{CPT}}(x_1)\, p_{\text{CPT}}(x_2 \mid x_1)\, p_{\text{CPT}}(x_3 \mid \cancel{x_1}, x_2)\, p_{\text{CPT}}(x_4 \mid \cancel{x_1}, \cancel{x_2}, x_3)\]

따라서 Joint Probability에 대한 식은 위와 같이 바로 이전 state에 대해서만 표현하면 되고, 이는 입력의 총 길이 n에 비례하는 파라미터만 사용하면 된다.

다만 해당 가정이 성립하지 않으며 모델의 깊이가 매우 얕기 때문에 Representation Learning이 불가능하다는 단점이 있어 쓰이지 못한다.

2.3 Parametric Neural Network

지금 사용하는 자기회귀모형은 $p(x_1, x_2, x_3, x_4)$ 값을 계산하는 과정에서 조건부 식들을 parameterize하는 과정을 거쳐 압축적으로 확률 값을 연산한다.

\[\begin{cases}p_{\text{Neural}}(x_2 \mid x_1;\alpha^2) = \sigma(\alpha_0^2 + \alpha_1^2 x_1)\\p_{\text{Neural}}(x_3 \mid x_1, x_2;\alpha^3) = \sigma(\alpha_0^3 + \alpha_1^3 x_1 + \alpha_2^3 x_2)\end{cases}\]

위와 같은 예시를 통해서 조건부 변수들의 값을 활용하여 새로운 변수에 대한 확률값을 근사하도록 설정하고 최종적으로 아래 식으로 Chain Rule 방식과 동일한 연산을 거친다.

\[p(x_1, x_2, x_3, x_4) \approx p(x_1)\, p(x_2 \mid x_1)\, p_{\text{Neural}}(x_3 \mid x_1, x_2)\, p_{\text{Neural}}(x_4 \mid x_1, x_2, x_3)\]

이는 각 step 별로 n개에 비례하는 파라미터가 요구되며 전체적으로는 $O(n^2)$ 파라미터를 사용하게 되므로 Chain Rule을 사용하는 방식보다 훨씬 경제적이며 Representation Learning이 가능하다.

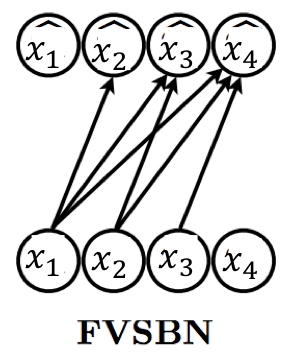
3. Fully Visible Sigmoid Belief Network(FVSBN)

2.3 Parametric Neural Network에 해당하는 생성형 모델 중 하나가 FVSBN이다. 유명한 흑백 이미지 데이터셋인 MNIST 데이터를 활용하면 이 모델을 잘 이해할 수 있다. MNIST 데이터셋은 28x28 크기의 이진 픽셀을 가진 이미지 데이터로 구성되어 있고, 개별 이미지는 $x \in [0, 1]^{(28 \times 28)}$로 표현 가능하다.

FVSBN을 이해하기 위해서는 Sequence Data로 간주해야 하기 때문에 (28, 28) 크기의 행렬 값을 (768, )벡터로 변환해주고 사용해야 한다. 초창기 Autoregressive model에 해당하는 FVSBN은 조건부 확률을 매개변수화해서 사용한다. 수식을 다시 작성해보면 아래와 같다.

\[p(x_1, \dots, x_{784}) = p_{\text{CPT}}(x_1; \alpha^1)\,p_{\text{logit}}(x_2 \mid x_1; \alpha^2)\,p_{\text{logit}}(x_3 \mid x_1, x_2; \alpha^3) \cdots p_{\text{logit}}(x_n \mid x_1, \dots, x_{n-1}; \alpha^n)\]

위 수식 각각을 풀어서 작성해보면 아래와 같이 표현할 수 있다.

\[p_{\text{CPT}}(X_1 = 1; \alpha^1) = \alpha^1, \quad p_{\text{CPT}}(X_1 = 0; \alpha^1) = 1 - \alpha^1\] \[p_{\text{logit}}(X_2 = 1 \mid x_1; \alpha^2) = \sigma(\alpha_0^2 + \alpha_1^2 x_1)\] \[p_{\text{logit}}(X_3 = 1 \mid x_1, x_2; \alpha^3) = \sigma(\alpha_0^3 + \alpha_1^3 x_1 + \alpha_2^3 x_2)\]

가장 첫번째 pixel 값에 해당하는 $p_{CPT}$ 값만을 제외하고 나머지는 모두 sigmoid 함수로 마지막 activation으로 변환해준 것을 확인할 수 있다. 앞에서 언급했듯이 i번째 pixel 값을 예측하기 위해서 i개의 파라미터를 사용하는 꼴이 되므로 $\Sigma_{i = 1}^{N} i$개의 파라미터만을 사용하며 Big-O Notation 상으로는 $O(n^2)$ 정도의 복잡도로 최적화가 가능해진다.

수식 뿐만 아니라 위 도식으로도 쉽게 이해가 가능하다. i번째 예측을 위해 1 ~ i-1번째 데이터를 사용하는 간단한 도식이다. 따라서 Training 또한 쉽게 진행할 수 있다. 이후에 데이터를 생성하는 과정에서는 아래와 같이 각각의 $\hat x_i$ 값을 0, 1 중에서 가능도가 높은 것들 중 하나로 classification하는 과정을 거치는 것이다.

\[\hat{x}_n \sim p_{\text{logit}}(X_n = k \mid x_1, x_2, ..., x_{n-1}; \alpha^n)\]

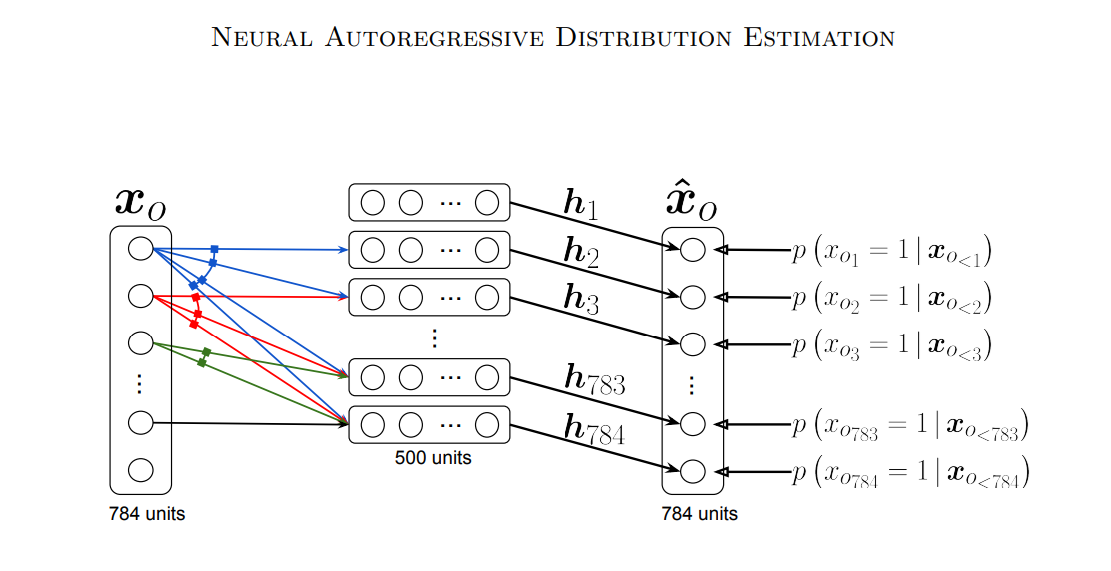
4. Neural Autoregressive Distribution Estimation(NADE)

FVSBN 모델은 각 input data에 대응하는 하나의 weight값을 할당해주는 방식으로 이루어져 있었다. NADE 방법은 input data sequence를 hidden vector 형태로 변환하여 더 많은 파라미터를 사용한 예측을 수행하는 모델이다. 이는 아래 그림을 통해서 더 잘 이해할 수 있다.

예측하려는 값을 $\hat x_{o_{k}}$로 표현하고 이전까지의 input값을 $\hat x_{o_{<k}}$로 표현하는 것인데, 이는 FVSBN과 동일한 구조이다. 다만, 중간에 hidden unit으로 전환한 이후 예측을 진행하는 것을 확인할 수 있다. 구체적인 수식은 아래와 같이 표현된다.

\[h_d = \sigma \big( W_{\cdot, o_{<d}} x_{o_{<d}} + c \big)\] \[p(x_{o_d} = 1 \mid x_{o_{<d}}) = \sigma \big( V_{o_d, :} h_d + b_{o_d} \big)\] \[W\in\mathbb{R}^{H\times D},\quad c\in\mathbb{R}^{H},\quad V\in\mathbb{R}^{D\times H},\quad b\in\mathbb{R}^{D}\]

4.1 Processing without Parameter Sharing

NADE 방법론에서는 Parameter Sharing을 도입하여 연산량을 최소화했다. 다만 먼저 파라미터 공유를 하지 않는 방식에 대해서 다루어보자. $h_d$인 hidden vector로 변환하기 위해서 W 값을 곱해주는데 표기에서 알 수 있듯이 x input의 길에 맞추어 H x 1 크기의 hidden vector로 변환하는 과정을 거치게 된다. $h_d$ hidden vector들은 전부 동일한 크기를 가지게 되고