Reinforcement Learning An Introduction - Ch.2 Multi Armed Bandits

Chapter 2 - Multi-arm Bandits

이 책의 1부에서는 먼저 정확한 해를 찾을 수 있는 간단한 경우를 다룬다. 이번 2장에서는 Bandit problem의 특수한 해를 다룬다고 한다.

Reinforcement Learning과 다른 학습 방법론들의 가장 큰 차이점은 바로 Evaluative Feedback를 사용한다는 것이다. 다른 학습 방법들이 어떻게 행동해야 할까라는 Instructive Feedback을 사용하는 것과 대비되는 것이 가장 큰 차이점이다. Evaluative Feedback은 본인이 수행한 Action이 최악인지 최선인지는 알 수는 없지만 Action이 얼마나 좋은 지에 대한 정보를 가진다.

2장에서는 실제 강화학습에서 다루는 복잡한 설정이 아닌 이해를 위한 간단한 설정을 둔다.

• Nonassociative setting
• Stationary reward
• N-armed bandit problem

위 Multi-armed bandit 구조는 state는 고정되어 있고 action에 따른 단기적인 Reward $R_{t+1}$만을 고려하는 상황이다. RL에서는 한 state에서의 action이 다음 state와 reward에 영향을 미치는 것이 차이점이다.

2.1 N-armed Bandit

N-armed Bandit은 N개의 선택지를 가지는 slot machine에서 옵션들 중 하나를 선택하는 문제를 1000번 반복하여 숫자로 된 보상의 총 합을 최대화하는 문제로 생각할 수 있다.

Nonassociative setting이기 때문에 각 action에 해당하는 실제 value값이 필요햐다. 이를 수식으로 표현하면 아래와 같다. 일반적인 state-action value function에서 state 항을 고정시켜 표현할 수 있다.

\[q_*(a) \;\triangleq\; \mathbb{E}\!\left[ R_t \mid A_t = a \right]\]

다만 실제 action value function을 구할 때에는 $R_t$가 아닌 $G_t$를 사용해야 함에 유의하자. 책에서는 t 시점에서의 action으로 인한 reward를 $R_t$로 설정하고 진행한다. 저 식은 모든 Action의 실제 가치에 대한 식이지만, 실제로는 value를 추정할 수 있어야 하며, t 시점에서 action $a$에 대한 추정값은 $Q_t(a)$로 표현한다.

$Q_t(a)$와 $q_*(a)$의 차이가 작을수록 학습이 잘 될 것이며, 이 추정과 관련하여 어떤 action을 선택해야 하는지에 대한 논의가 이어진다. 강화학습 문제에서 Exploration과 Exploitation간의 균형이 중요하다고 했는데, 이 문제에서 Exploration은 매 시점 $\underset{a}{\operatorname{argmax}} Q_t(a)$를 만족하는 action을 선택하는 것이고, Exploitation은 해당 action이 아닌 다른 action을 선택하는 것을 의미한다.

단기적으로는 Exploitation을 사용하는 것이 최대 Return을 가져다 주지만, Exploration이 있어야 Non-stationary reward를 주는 상황에서도 대처가 가능하고 장기적으로 더 큰 Return을 받을 수 있다. 이 선택과 관련하여 여러 prior distribution을 활용한 접근이 있었지만 해당 사전 분포가 존재함을 보장할 수 없다면 제대로 된 해결이 불가능하게 된다. 이 책에서는 이 Balancing Strategy는 깊게 다루지 않지만, Exploitation을 계속하는 것보다는 Balancing이 도움이 된다고 강조한다.

2.2 Action Value methods

후술하는 장에서는 이 간단한 문제를 해결하는 여러 방법에 대해서 소개한다. Action value method는 action의 value를 추정하여 action을 선택하도록 하는데, $q_*(a) \;\triangleq\; \mathbb{E}!\left[ R_t \mid A_t = a \right]$ 이라는 value의 수식에 맞추어 $Q_t(a)$를 다음과 같이 추정하고 이를 표본평균(Average) 방법이라고도 한다. 아래 식에서 $N_t(a)$는 t 시점 이전까지 action a를 수행한 횟수를 의미한다.

\[Q_t(a) \;=\; \frac{R_1 + R_2 + \cdots + R_{N_t(a)}}{N_t(a)}\]

추정한 Value를 바탕으로 Action을 선택해야 하는데, Greedy Policy에 따르면 가장 높은 Value를 가지는 Action을 선택하는 것이며 이때 선택하는 Action $A_t$는 $A_t \;=\; \arg\max_{a} Q_t(a)$ 로 표현한다. 이 Policy를 가지고 진행한다면, 결국 초기에 긍정적으로 평가를 받은 Action만 연속해서 평가하여 나머지 Action에 대해서 제대로 된 value를 추정하지 못하는 문제가 발생할 수 있다.

이를 보완하기 위한 방법으로 $\epsilon$-greedy policy를 생각해 볼 수 있다. 작은 엡실론 만큼의 확률 만큼은 다른 action을 시도하도록 하여 시행을 무한히 많이 진행하면 실제 $q_*(a)$에 수렴하도록 할 수 있다.

\[A_t = \begin{cases} \arg\max_a Q_t(a), & \text{with probability } 1-\varepsilon \\ \text{random action}, & \text{with probability } \varepsilon \end{cases}\]

2.3 10-armed bandit

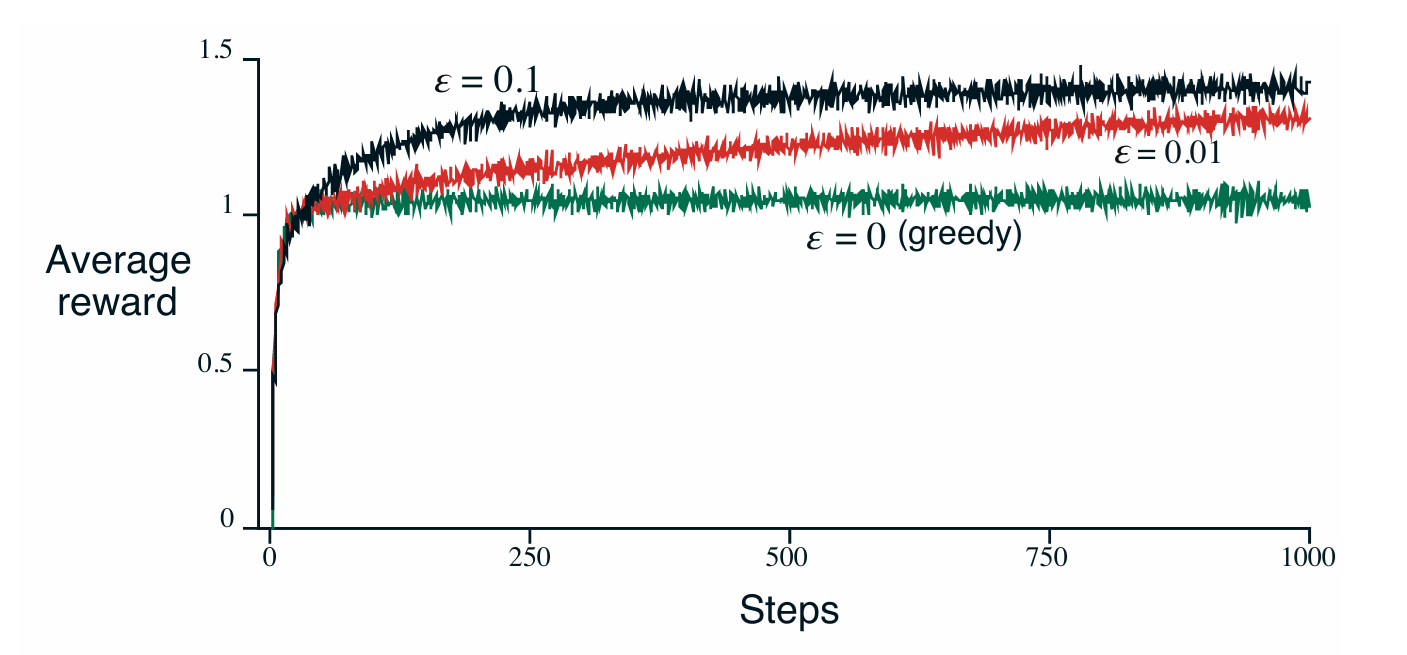
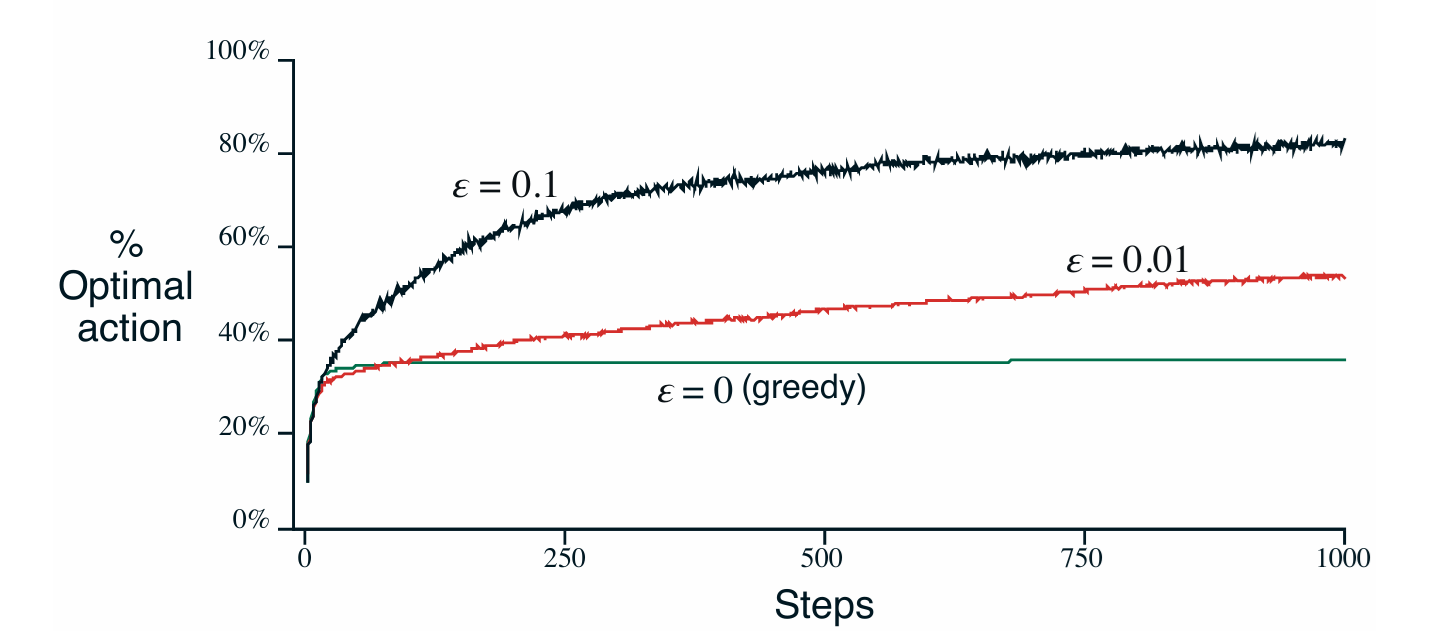
선택이 10개인 bandit problem을 1000번 반복하여 합을 최대화화는 예제 2000쌍을 준비하여 실제로 학습을 시켜보자. 10개 각각의 action은 np.random.normal(0, 1, 10)으로 실제 action value 값으로 설정했다. 다만 매 step마다 실제 reward를 뽑을 때에는 np.random.normal(q(a), 1)로 설정하여 noise를 추가한 형태로 평가를 진행한다.

위 설정을 바탕으로 greedy, $\epsilon$-greedy ($\epsilon$ = 0.1), $\epsilon$ - greedy($\epsilon$ = 0.01)의 성능을 비교한 그림이 아래와 같다.

Greedy Policy를 사용하는 경우 초기에는 빠른 reward 상승을 이루었으나 suboptimal 수준에 가지는 경우가 대부분이기 때문에 실제 optimal action을 반복하는 비율은 30% 정도에 그쳤다.

다만 $\epsilon$ 값이 0.01이냐 0.1이냐 따라서도 실제 optiaml action의 비율이 달라졌지만 이는 문제에 따라 다른 것이기 때문에 절대적인 수치는 중요하지 않다. 실험에서 설정한 Reward의 분산이 커진다면 엡실론 값이 커질 수록 유리할 것이고 분산이 작다면 엡실론 값이 작은 것이 유리할 것이기 때문이다. 극단적으로 분산이 0인 random sampling을 진행하더라도 $q_*(a)$의 값이 Time-varient한 경우라면 당연히 $\epsilon$값이 큰 것이 유리할 것이다.

2.4 Incremental Implementation

위 표본평균 방식으로 Value function을 추정할 때, 아래 식을 사용했다.

\[Q_t(a) \;=\; \frac{R_1 + R_2 + \cdots + R_{N_t(a)}}{N_t(a)}\]

위 식을 통해서 Value 값을 추정할 때 실제로 모든 sequence Reward 값을 가지고 있는 것은 굉장히 비효율적이다. 아래 수식을 통해서 확인할 수 있듯이, 이전값, 새로운 update 값을 활용하여 효율적으로 average 값을 update할 수 있다. k번째 선택까지의 Value 추정값은 $Q_{k+1}$이라 설정한 것이다.

\[Q_{k+1} \;=\; \frac{1}{k}\sum_{i=1}^{k} R_i\] \[\begin{aligned} Q_{k+1} &= \frac{1}{k} \left( R_k + \sum_{i=1}^{k-1} R_i \right) \\[6pt] &= \frac{1}{k} \left( R_k + (k-1)Q_k \right) \\[6pt] &= \frac{1}{k} \left( R_k + kQ_k - Q_k \right) \\[6pt] &= Q_k + \frac{1}{k}\left( R_k - Q_k \right) \end{aligned}\]

Average method에서는 $\frac{1}{k}$ 라는 파라미터를 사용하여 Q 값을 Update할 수 있지만 실제로는 아래와 같이 일반화하여 Update를 진행할 수 있다. $\text{New estimate} = \text{Old estimate}+\text{Step size} \times \text{Error}$ 위 식은 TD-Learning 등등에서 매우 자주 등장한다.

2.5 Non-stationary Problem

이 장의 가정들 중에서 Stationary reward 가정이 있었다. 이는 보상값의 확률 분포가 유지된다는 조건이었는데, 이 조건을 없앤다면 시간에 따라서 보상값이 추출되는 분포가 달라지게 될 것이다.

그렇게 된다면 최근에 생성된 정보일수록 더 많은 가중치를 주어 Update해야 한다는 것을 의미한다. $Q_{k+1}= Q_k + \frac{1}{k}\left( R_k - Q_k \right)$의 수식만 해도 기존의 정보는 $1 - \frac{1}{k}$의 비율로, 새로운 정보는 $\frac{1}{k}$비율로 새로운 Q 값에 영향을 주는 것을 확인할 수 있다. 이때의 비율은 파라미터를 통해서 조절할 수 있다.

고정값 $\alpha$를 통해서 수식을 새롭게 작성했다고 가정해보자.

\[\begin{aligned} Q_{k+1} &= \alpha R_k + (1-\alpha)Q_k \\[4pt] &= \alpha R_k + (1-\alpha)\bigl[\alpha R_{k-1} + (1-\alpha)Q_{k-1}\bigr] \\[4pt] &= \alpha R_k + (1-\alpha)\alpha R_{k-1} + (1-\alpha)^2 Q_{k-1} \\[4pt] &= \alpha R_k + (1-\alpha)\alpha R_{k-1} + (1-\alpha)^2 \alpha R_{k-2} + \cdots \\[4pt] &\quad + (1-\alpha)^{k-1}\alpha R_1 + (1-\alpha)^k Q_1 \end{aligned}\]

이렇게 된다면 새로운 Reward일수록 더 큰 가중치를 가지게 되고, 각각의 Reward 값과 Initial value에 적용된 가중치들을 모두 더하면 1이 되기 때문에 이를 Exponential Receny-weighted Average라고 부른다.

다만 $\alpha$ 모두에 대해서 목적값이 수렴하지는 않는다. 확률론적 근사 이론에 따르면 반드시 수렴하기 위한 조건은 아래 두가지로 정리된다. 이때 $\alpha_n(a)$는 행동 a를 n번째 진행할 때의 파라미터를 의미한다.

\[\sum \alpha_n(a) = \infty, \sum \alpha^2_n(a) < \infty\]

$\alpha_n(a)$가 $\frac{1}{n}$인 경우, 두 식을 만족하지만 수렴 속도가 매우 느리다는 단점이 있기에 stationary한 경우 좋고 $\alpha_n(a)$가 상수로 고정되어 있다면 두번째 조건에 의해서 수렴성이 보장되지 않지만 nonstationary reward를 주는 경우에 제대로 동작한다.

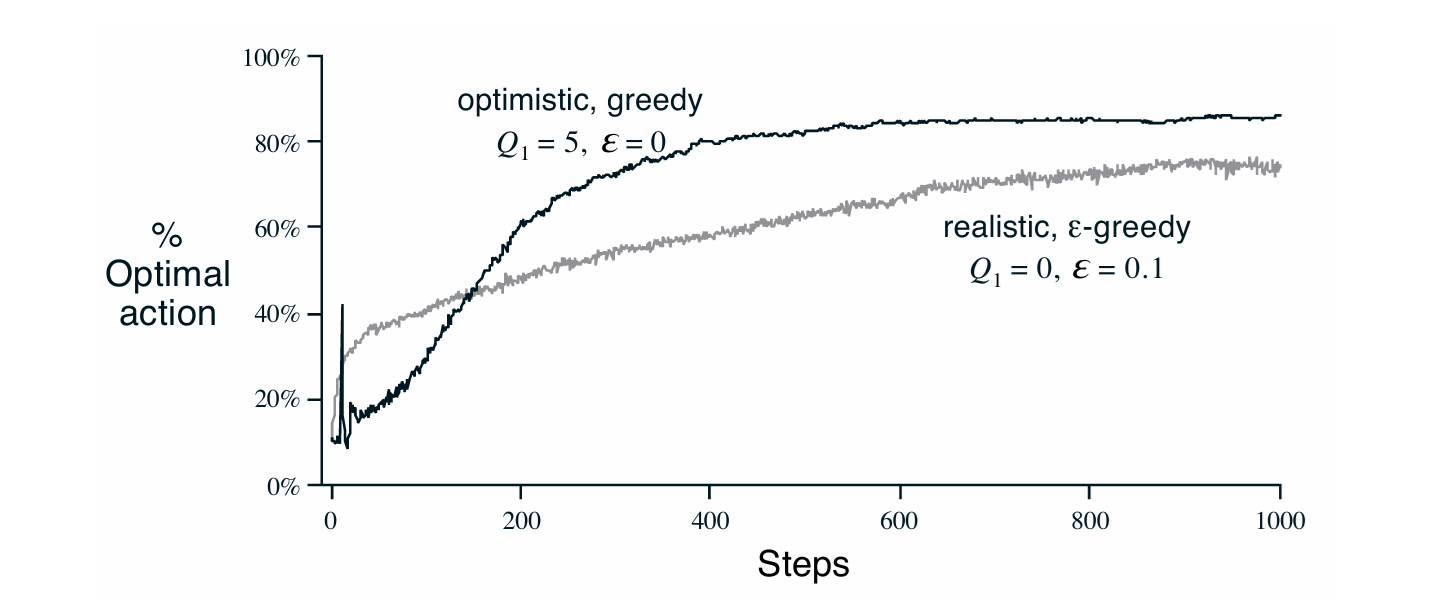
2.6 Optimistic Initial Values

지금까지 살펴본 모든 Policy는 초기 추정값 $Q_1(a)$에 의해 Bias가 생긴다는 단점이 있다. 물론 한번 action이 선택되면 Unbias해지지만, 초기에는 영향을 미치기 때문에 이를 잘 활용한다면 더 빠른 수렴을 유발할 수 있다.

단적인 예시로 $Q_1(a)$의 값을 전부 5로 설정하게 된다면, np.random.normal(0,1)에서 추출한 값이라고 할 때 굉장히 큰 z 값을 가질 것이다. 따라서 Greedy policy를 사용한다고 가정해도 어떤 action을 취하던 reward가 5보다 굉장히 작을 것이기 때문에 초반에 Exploration을 진행한다는 장점이 있다. 다만 이 탐험은 초반에만 영향을 주기 때문에 Non-stationary reward에 대해서는 별다른 이득이 없다.

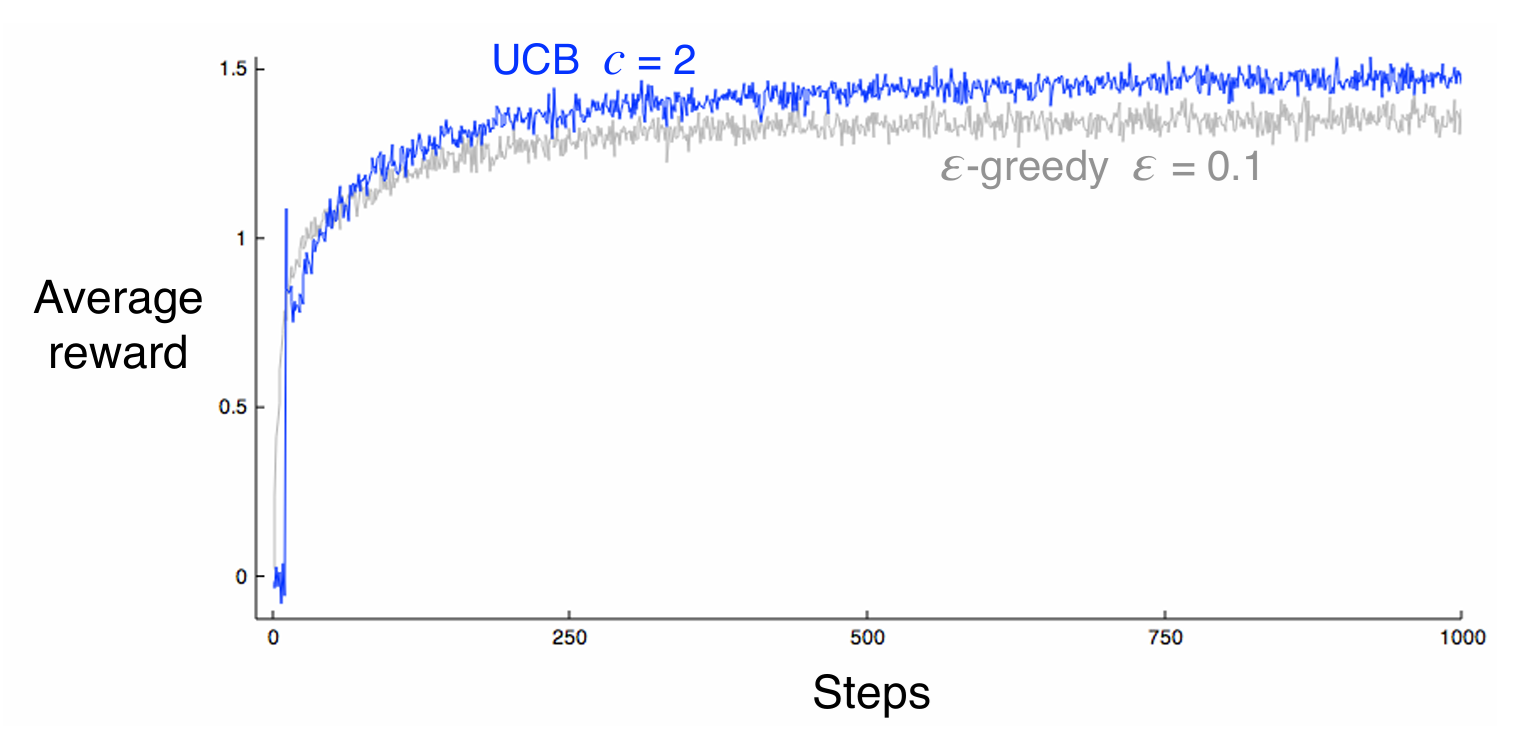
2.7 Upper-Confidence-Bound Action Selection

지금까지 살펴본 전략은 2가지이다.

• Greedy Policy : 단기적으로는 효용, 장기적으로는 확실치 않음
• $\epsilon$-Greedy Policy : 탐색을 강제하지만, 선택지를 Random Choice 한다.

엡실론 그리디 전략을 생각해보면, 모든 action을 동일선 상에서 비교한다. 분명히 Non-optimal Choice에도 좋고 나쁨이라는 것은 존재하는데, 이를 반영하지 않고 뽑는 것은 문제가 있다. |Max value - Value|, Uncertainty, Confidence 등등을 모두 반영해서 뽑는 것이 바람직하다는 의견이 있었고, 이를 UCB(Upper-confidence-bound / 신뢰 상한)이라고 부른다.

$t$ 시점에서 선택하는 Action을 $A_t$라고 한다면, 선택하는 Action은 아래 수식을 따른다.

\[A_t \;=\; \arg\max_{a} \left[ Q_t(a) \;+\; c \sqrt{\frac{\ln t}{N_t(a)}} \right]\]

선택되지 않는 Action이라면 $\ln t$는 커지고 $N_t(a)$는 작아지기 때문에 뽑힐 확률이 증가하고 선택되는 Action이라면 $\ln t$는 커짐에 따라 $N_t(a)$또한 커지기 때문에 상대적으로 비교하는 argmax 특성상 뽑힐 확률이 적어지는 효과를 낳는다. 이때 $c$는 상한의 신뢰수준이라고 한다.

위 plot은 앞의 10-armed bandit 예시에 UCB를 적용한 모습을 보여준다. 이 예시에서는 간단하기 때문에 UCB가 더 좋은 성능을 보이지만, 신뢰 수준을 간단한 방식으로 표현 UCB 방법은 State space가 커지거나 난이도가 높은 문제에서는 적용하기 어렵다.

2.8 Gradient Bandits

지금까지의 방법은 Value를 Estimate하고, 이를 바탕으로 Action을 선택하는 고정된 Policy를 사용했다. 다만, Value를 사용하지 않고, 고정되지 않은 Policy를 사용하는 방법도 존재한다.

먼저 각 Action a에 대한 상대적 선호도를 나타내기 위한 파라미터 $H_t(a)$를 정의하자. 이는 Reward를 의미하는 것은 아니며, action a가 선택될 확률 $\pi_t(a)$ 에 영향을 미친다.

\[\pi_t(a) = \frac{e^{H_t(a)}}{\sum_b e^{H_t(b)}}\]

Action a가 선택될 확률이 $\pi_t(a)$일 때, 우리가 최대화화려는 목적식은 $E[R_t]$로, $\Sigma_x \pi_t(x)q_*(x)$과 동치이다. 이 수식을 통해서 우리가 원하던 목적식을 Value Estimation 없이 표현할 수 있고, Problem에 맞는 Policy를 직접 찾을 수 있다. 이는 Gradient Ascent 방식을 통해서 Update하는 것이 가능하기 때문이다.

우리가 최종적으로 Update해야 하는 Policy는 $H_t(a)$와 연관이 있기에, Update 식은 아래와 같다.

\[H_{t+1}(a)=H_t(a)+\alpha\frac{\partial \mathbb{E}[R_t]}{\partial H_t(a)}\]

위에서 언급한 $E[R_t]$의 식을 대입하면 아래와 같다.

\[\begin{aligned} \frac{\partial \mathbb{E}[R_t]}{\partial H_t(a)} &= \frac{\partial}{\partial H_t(a)} \left[ \sum_b \pi_t(b)\, q_*(b) \right] \\[6pt] &= \sum_b q_*(b)\, \frac{\partial \pi_t(b)}{\partial H_t(a)} \\[6pt] &= \sum_b \bigl(q_*(b) - B_t\bigr) \frac{\partial \pi_t(b)}{\partial H_t(a)} \\[6pt] &= \sum_b \pi_t(b)\bigl(q_*(b) - B_t\bigr) \frac{\partial \pi_t(b)}{\partial H_t(a)} \Big/ \pi_t(b) \end{aligned}\]

이때 $B_t$는 새로 나온 보상을 비교할 수 있는 비교대상이 되며, $\pi_t(b)$의 합이 모두 1이 되기 때문에 상수에 대한 $H_t(a)$의 편미분값은 0이라는 것을 반영하면 추가 전후의 식은 동일하다.

\[= \mathbb{E} \left[ \bigl(q_*(A_t) - B_t\bigr) \frac{\partial \pi_t(A_t)}{\partial H_t(a)} \Big/ \pi_t(A_t) \right]\]

위 식을 기댓값의 식으로 바꾸기 위해서 $x$ 대신 R.V. $A_t$를 도입했다.

\[= \mathbb{E} \left[ (R_t - \bar{R}_t) \frac{\partial \pi_t(A_t)}{\partial H_t(a)} \Big/ \pi_t(A_t) \right] \tag {2.1}\]

$\mathbb{E}[q(A_t)]=\mathbb{E}\bigl[\mathbb{E}[R_t \mid A_t]\bigr]$의 수식은 Law of Total Expectation에 의해서 $\mathbb{E}\bigl[\mathbb{E}[R_t \mid A_t]\bigr]=\mathbb{E}[R_t]$ 표현가능. 추가적으로 비교의 대상을 기존 모든 Reward의 평균인 $\bar{R}_t$로 설정하면 무리 없는 비교가 가능하다.

\[\frac{\partial \pi_t(b)}{\partial H_t(a)}=\pi_t(b)\bigl(\mathbb{I}_{a=b} - \pi_t(a)\bigr),\]

식 2.1에서의 편미분값을 살펴보면, Softmax 미분값이기 때문에 위 식과 같이 표현할 수 있고, 전체 식을 정리하면 아래와 같다. 이는 자명하므로 바로 사용할 수 있다.

\[\begin{aligned} \frac{\partial \mathbb{E}[R_t]}{\partial H_t(a)} &= \mathbb{E} \left[ (R_t - \bar{R}_t)\, \pi_t(A_t) \bigl(\mathbb{I}_{a=A_t} - \pi_t(a)\bigr) \Big/ \pi_t(A_t) \right] \\[6pt] &= \mathbb{E} \left[ (R_t - \bar{R}_t) \bigl(\mathbb{I}_{a=A_t} - \pi_t(a)\bigr) \right]. \end{aligned}\]

위 식을 최종적으로 Gradient Ascent 식에 대입하면 아래와 같다.

\[H_{t+1}(a) = H_t(a) + \alpha (R_t - \bar{R}_t) \bigl(\mathbb{I}_{a=A_t} - \pi_t(a)\bigr), \qquad \forall a\]

위 식은 결과적으로 Gradient Ascent Algorithm에 따라서 최종적인 목적식을 최대화하는 과정을 보여주는 것이기 때문에 원하는 목적으로의 강건한 수렴성을 보장한다. 알고리즘을 통해서 Value function 을 직접 사용하지 않고도 문제를 푸는 방식을 확인할 수 있었고, Policy 또한 문제에 맞게 최적화할 수 있음을 확인할 수 있었다.

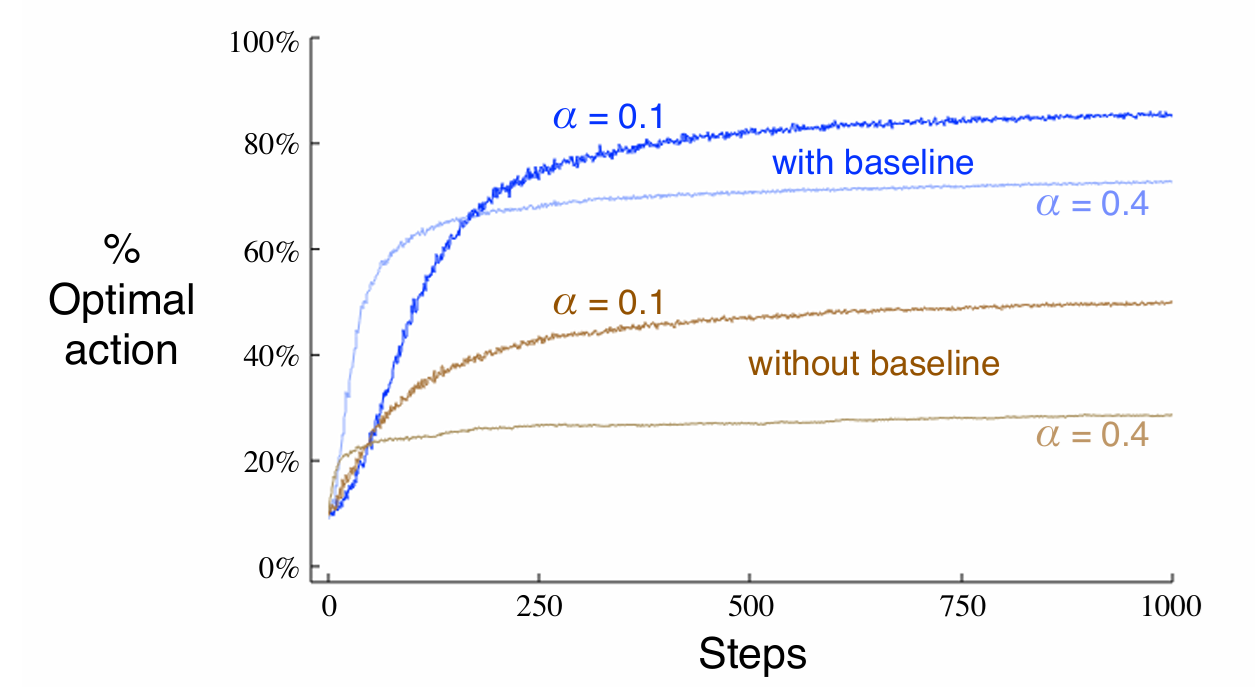
추가적으로 동일한 Learning rate를 사용하고도 비교 대상이 있냐 없냐에 따라서 알고리즘의 효율성이 달라짐을 확인할 수 있다. Update 식을 통해서 확인해보면 평균적인 보상보다 작으면 선택된 action의 선호도가 감소하고 나머지의 선호도가 올라가지만, 평균적인 보상보다 높으면 선택된 action의 선호도는 증가, 나머지는 감소하기 때문이다. 적절한 Baseline을 통한 최적화 또한 중요하다.

이 내용은 추후 공부할 13. Policy Gradient와도 연관된다.

2.9 Associative Search

지금까지는 Nonassociative 한 경우만을 다루었다. 다시 말해서 현재의 Action이 다음 state나 reward에는 영향을 미치지 않는 경우를 다루었는데, 이 경우라면 우리가 앞에서 살펴본 내용들은 거의 잘 동작하지 않는다. 이때는 추가적인 정보를 활용하여 학습을 진행해야 하며 완전한 RL 문제를 다루기 위해서는 Future State, Future Reward를 모두 고려해야 한다.

2.10 Summary

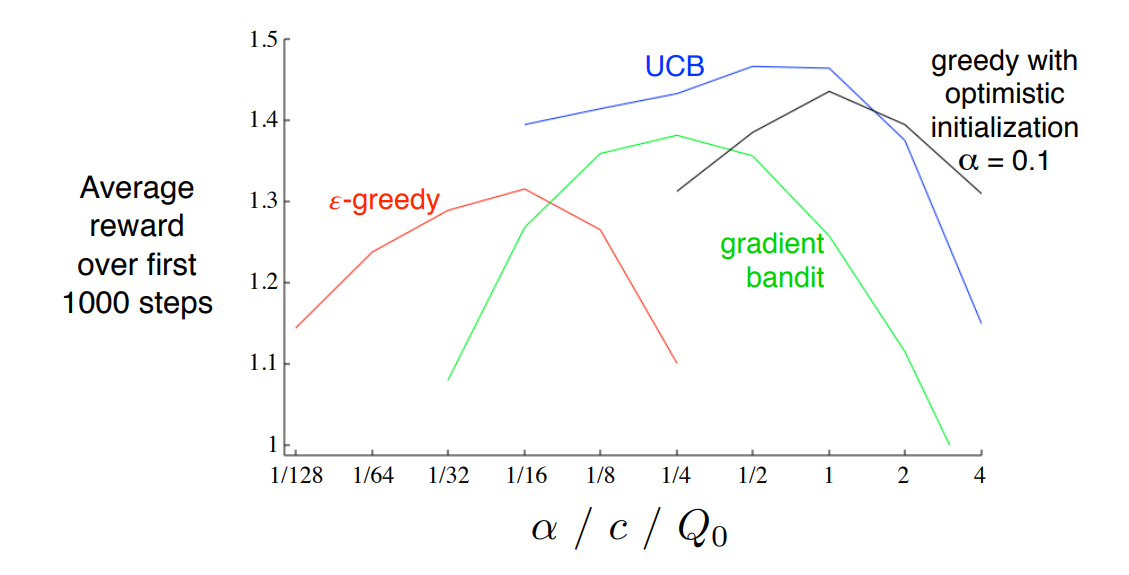
이 장에서는 간단한 Nonassociative setting에 대해서 Greedy, Epsilon-Greedy, UCB, gradient ascent 방법을 활용하여 탐험과 활용 사이의 균형을 맞추는 방법을 다루었다. 각각의 방법을 비교하는 것은 물론 문제에 따라 다르고 적합한 방식이 다르기 때문에 크게 의미는 없다고 생각한다. 다만 책에서는 Parameter Study로 각 파라미터 별 평균 보상의 성능을 측정해두었다.

Multi armed bandit 문제에서 Exploration과 Exploitation 사이의 균형을 잡는 연구는 계속해서 이루어져 왔다. 이번 장에서 설명한 방법 말고도 수많은 방법이 있지만 저자는 복잡한 방법은 실제 강화학습 연구와 잘 맞지 않으며 오히려 간단한 방법들을 일부 사용한다고 한다. Gittins index라고 부르는 방법론도 마찬가지로 특별한 경우에 대해 곧바로 균형점을 계산할 수 있지만 이는 매우 특수한 경우만 해당한다.