Chapter 3 - Finite Markov Decision Process
Finite Markov Decision Process, 유한 마르코프 결정 과정은 2장에서 언급한 Evaluative Feedback을 사용한다. 하지만 여기에 추가로 associative aspect가 추가되어 현재 state에서의 Action이 다음 state 나 reward에 영향을 주기 때문에 즉각적인 Reward $R_{t+1}$ 뿐만 아니라 지연된 보상까지 고려해야 한다.
2장을 다룰 때에는 $q(a)$ 만을 다루었지만 이제 상태 정보를 추가하여 더 정확한 value를 표현해야 한다. $q(s, a)$는 Action-Value Function $v(s)$는 State-Value Function이라고 부른다. 이번 장에서 소개하는 Finite Markov Decision Process는 강화학습 문제를 이론적으로 정교하게 설명할 수 있도록 해주는 이상적인 수학적 형태이다.
3.1 The Agent–Environment Interface
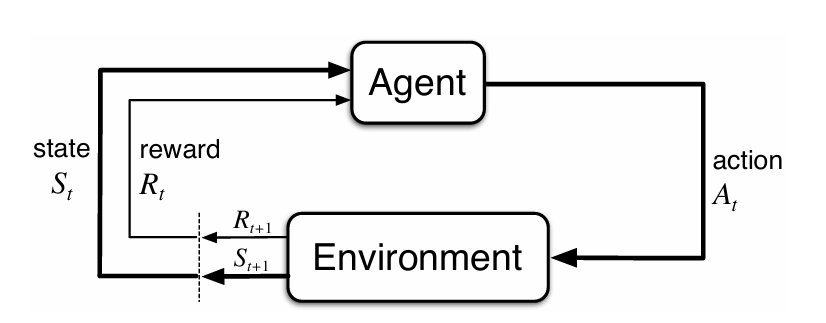
위 Plot은 MDP의 Agent와 Environment간의 상호작용을 잘 나타낸다. Agent는 현재 State $S_t$에서 Action $A_t$를 취하면 환경은 이에 대응하는 다음 State $S_{t+1}$과 해당 ($S_t$, $A_t$) Pair에 대응하는 즉각적인 보상 $R_{t+1}$을 제공해준다. 위 과정이 계속해서 반복적으로 일어나며 상호작용하며 MDP와 Agent는 State, Action, Reward의 Sequence인 Trajectory를 생성해 낸다. (Trajectory는 $S_0 \; A_0 \; R_1 \; S_1, \; A_1 \; …$ 등등으로 표현될 수 있는 순열을 의미한다.)
유한 마르코프 결정 과정에서는 상태(S), 행동(A), 보상(R) 집합은 항상 유한한 값의 숫자 원소를 갖고 있다. 또한 확률 변수 $R_t$와 $S_t$는 오로지 이전 상태와 행동에 의존하는 이산 확률 분포를 갖는다는 점을 기억해야 한다. 이를 수식으로 표현하면 아래와 같이 표현할 수 있다.
\[p(s', r \mid s, a) \;=\; \Pr\{ S_t = s',\; R_t = r \mid S_{t-1} = s,\; A_{t-1} = a \} \tag{3.1}\]$R_t$와 $S_t$는 위와 같이 이전 State와 Action이 주어진다면 확률 분포가 정해지는 것이고, 확률 분포의 성질에 의해서 가능한 모든 reward과 state 조합을 합하면 1이 되는 것은 자명한 사실이다. (이 장에서는 Finite MDP를 상정하고 있기 때문에 적분이 아닌 $\Sigma$를 사용해야 한다.)
\[\forall s \in \mathcal{S},\; a \in \mathcal{A}(s), \qquad \sum_{s' \in \mathcal{S}} \sum_{r \in \mathcal{R}} p(s', r \mid s, a) = 1\]다만 위의 식을 곰곰히 생각해보면 이상한 점이 존재한다. 분명히 Associative Aspect에 의해서 현재 상태에서의 Action이 미래의 모든 State와 Reward에 영향을 미쳐야 한다고 했는데, 저 조건식을 통해서 살펴본다면 바로 이전의 State와 Action에 의해서만 영향을 받는다는 것을 확인할 수 있다. 즉, 현재 State는 이전의 모든 State에 대한 정보를 가지고 있어야 한다는 것을 의미하며, 이 성질을 Markov Property라고 부른다. 이 책의 2부에서 이 가정에 구애받지 않고 근사적인 방법을 다룬다고 한다.
\[P[S_{t+1}|S_t] \; = \; P[S_{t+1}|S_t,...,S_1]\]또한 (3.1)의 식을 변형하면, 상태 전이 확률(State Transtion Probability)이나 보상의 기댓값을 계산할 수 있다.
\[p(s' \mid s, a)\;=\;\Pr\{ S_t = s' \mid S_{t-1} = s,\; A_{t-1} = a \} \;=\;\sum_{r \in \mathcal{R}} p(s', r \mid s, a)\] \[r(s, a)\;=\;\mathbb{E}[R_t \mid S_{t-1} = s,\; A_{t-1} = a]\;=\;\sum_{r \in \mathcal{R}} r \sum_{s' \in \mathcal{S}} p(s', r \mid s, a)\]위 기댓값 계산 과정을 더 자세히 표현하면 아래와 같이 미래 state에 대한 주변화를 통해 구할 수 있다.
\[\boxed{\begin{aligned}r(s,a)&=\mathbb{E}[R_t \mid S_{t-1}=s,\; A_{t-1}=a] \\ &=\sum_{r\in\mathcal{R}} r \;\underbrace{\Pr(R_t = r \mid s,a)}_{\displaystyle = \sum_{s'\in\mathcal{S}} p(s', r \mid s, a)}\end{aligned}}\]다음 State까지 고려하는 Reward는 아래와 같이 도출할 수 있다.
\[\begin{align}r(s,a,s')&\;\doteq\;\mathbb{E}\!\left[ R_t \mid S_{t-1}=s,\; A_{t-1}=a,\; S_t=s' \right] \\[6pt] &= \sum_{r\in\mathcal{R}} r \; \Pr\!\left( R_t = r \mid S_{t-1}=s,\; A_{t-1}=a,\; S_t=s' \right) \\[6pt] &= \sum_{r\in\mathcal{R}} r \; \frac{ \Pr\!\left( S_t=s',\; R_t=r \mid S_{t-1}=s,\; A_{t-1}=a \right) }{ \Pr\!\left( S_t=s' \mid S_{t-1}=s,\; A_{t-1}=a \right) } \\[10pt] &= \sum_{r\in\mathcal{R}} r \; \frac{ p(s', r \mid s, a) }{ \displaystyle \sum_{\bar r\in\mathcal{R}} p(s', \bar r \mid s, a) } \end{align}\]MDP 구조는 매우 추상적이고 유동적이기 때문에 많은 변주가 있을 수 있다.
- Agent와 Environment간의 상호작용 t가 유동적일 수 있다.
- Action의 범위가 정신적인 범위에서 물리적인 범위까지 다양할 수 있다.
- State 또한 정신적인 범위에서 물리적인 범위까지 폭넗게 존재할 수 있다.
MDP에서 Agent와 Environment 사이의 경계는 굉장히 모호하게 다가올 수 있으나, 이 경계는 Agent가 원하는 데로 조작할 수 있는 범위를 생각해보면 명확해진다. 사람과 외부 환경 사이의 상호작용에서도 근육이나 뼈대, 감각 기관은 Agent쪽에 속할 것으로 생각되지만, 어떻게 할 수 없는 것이기 때문에 환경으로 보아야 한다. 로봇의 모터나 특정 하드웨어 또한 환경에 의해서 변화되지만 결국 Agent가 원하는 데로 변화시킬 수 없는 것이기 때문에 결국 Environment 쪽으로 생각되어야 한다. 책에서는 여러 MDP 관련 예시가 있지만 재활용 로봇 예시를 바탕으로 3장의 내용을 정리해보겠다.
3.3 Recycling Robot
로봇은 빈 소다 캔을 모으는 일을 하고 있다. 로봇은 캔을 감지하는 센서와 캔을 집어서 자신의 몸통에 달린 쓰레기통에 버리기 위한 도구를 갖고 있다. 로봇은 재충전이 가능한 배터리로 작동한다.
예제를 단순화하기 위해서 아래와 같은 조건을 가정한다.
- State = {High, Low}
- Action = {Search, Wait, Recharge}
- A(High) = {Search, Wait} A(Low) = {Search, Wait, Recharge}
- Reward
- 대부분의 시간 동안은 0을 가짐.
- 빈 캔 하나를 확보하면 +1 보상을 가짐.
- 배터리가 다 되면 큰 -3 보상을 가짐.
- $r_{search}$ > $r_{wait}$에 해당하는 각각의 보상이 존재함.
- Details
- $P(High \mid High, Search) = a$
- $P(Low \mid High, Search) = 1 - a$
- $P(Low \mid Low, Search) = b$
- $P(High \mid Low, Search) = 1 - b$
위 예시에서 State, Action, Reward에 대한 식이 주어져 있기 때문에 이를 2가지 버전으로 표현할 수 있다. 먼저 전이 확률과 보상의 기댓값을 기록하는 것이 가능하다.
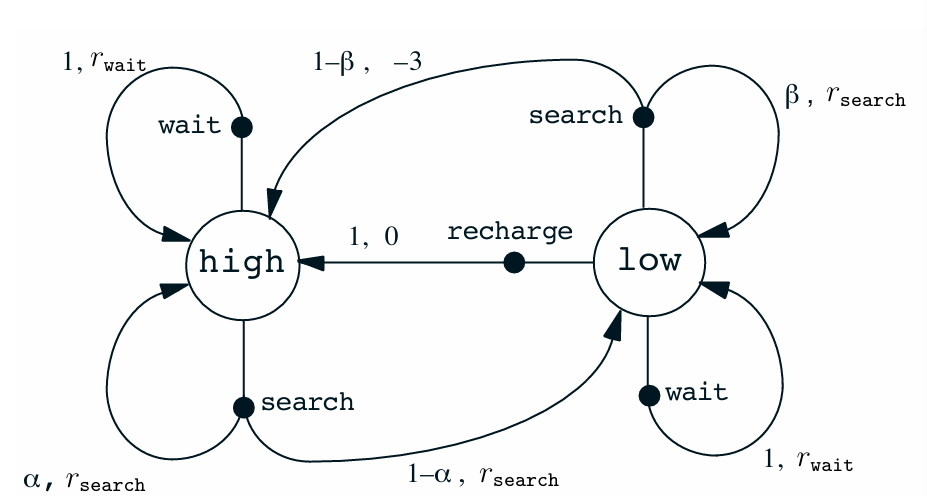
또 다른 방법은 State Transition Graph로 나타내는 것인데, State Node와 Action Node 2가지가 존재하며 이때 Action에 따른 $P(S \mid s, a)$ 와 $r(S, s, a)$ 가 Pair로 graph에 작성된다.
3.2 Goals and Rewards
강화학슴은 지도학습과 다르게 Agent의 목적이나 목표를 보상(Reward) 라는 특별한 신호로 형식화한다. 다만, 즉각적인 Reward가 아니라 모든 Reward들의 총합을 최대화하는 것이 최종 목표가 된다. 이를 보상 가설(Reward Hypothesis)이라고 부른다.
Agent에게 목적을 이루기 위해서 어떻게 해야 하는지를 알려주는 것이 아니라, 계속해서 어떤 것을 해야 하는가에 대한 정보를 주는 것이 RL이라고 볼 수 있다. 앞선 예시에서 쓰레기를 주웠을 때 +1의 보상을, 방전되었을 때 -3의 보상을 주는 것이 “무엇을” 해야 하는지에 대한 정보를 주는 것이라고 생각하면 된다.
3.3 Returns
앞서 이야기한 것처럼, Agent의 최종적인 목표는 Cumulative Reward sum을 최대화하는 것이다. 정확히는 기대되는 이득을 최대화하려고 하는 것인데 이득(Return)은 $G_t = R_{t+1} + R_{t+2}+…$으로 표현되는 보상의 총합을 의미한다. 이득은 문제에 따라서 Episodic Task와 Continuous Task로 나뉠 수 있다.
Episodic Task의 경우 Terminal State가 존재하기 때문에 이득이 무한대로 발산할 일은 없다. Episode라는 것은 게임처럼 끝이 명확하게 존재하고 계속해서 반복하는 구조를 의미한다. 이 식은 아래와 같이 표현할 수 있다.
Continuous Task의 경우 Terminal State라는 것이 명확하지 않고 계속해서 지속되는 경우에 해당한다. 사실 게임을 제외하고 나서는 대부분의 Task가 연속적이기 때문에, $G_t$가 시간이 지남에 따라서 무한히 커지는 것은 자명하다. 따라서 이를 방지하기 위해서 discount rate $\gamma$ ($0 \le \gamma \le 1$) 를 도입하여 미래 시점의 이득에 대한 정보를 줄이는 역할을 한다.
$\gamma$의 값이 0에 가까우면 myopic하게 가까운 시점의 reward에 집중하는 것이고, $\gamma$가 1에 가까우면 far-sight하게 미래 시점의 reward에 집중하는 것이라고 생각할 수 있다.
3.4 Unified Notation for Episodic and Continuing Tasks
앞선 3.3에서 Episodic Task과 Continuous Task의 Return에 대해 공부했다. 현실적으로 두 가지 모두 고려해야 하기 때문에 이를 통합적으로 표기하는 방법이 필요하다. Episode를 표기하기 위해서 $i$번째 Episode라는 것을 추가하여 $S_{t,i}$, $A_{t, i}$ 등등으로 표현하는 것이 가능하지만 이는 거의 사용되지 않고 특정한 하나의 Episode에 대해서 언급하거나 전체 Episode에 대해 이야기 할 때 Notation을 무시하고 $S_t, A_t$로 표기한다.
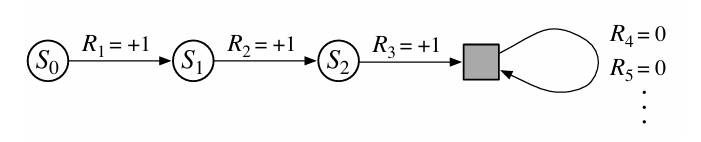
통합적인 Return 표기를 위해서 생각해보자면 Continous Task 형태에서 Episode를 표현하는 방법은 그저 Terminal State 이후의 Reward를 전부 0으로 설정하는 것을 생각해볼 수 있다. 이렇게 된다면 무한히 많은 time step을 고려하더라도 Episode를 표현할 수 있게 된다.
또한, $\gamma$ 값을 1로 표현한다면 Discount 없는 Reward Sum을 연산할 수 있기 때문에 이를 반영한 표기는 아래와 같으며, 앞으로의 식에서는 Return을 아래 식과 같이 표현할 것이라고 한다.
\[G_t\;\doteq\;\sum_{k=0}^{T-t-1} \gamma^{k} \, R_{t+k+1}\]3.5 Value Functions and Policy
Actor-Critic과 같은 특수한 경우를 제외한다면 거의 모든 강화학습 알고리즘은 Value Function을 사용한다. 우리가 어떤 행동이나 상태의 실제 가치를 정확하게 아는 것은 불가능하기 때문에, Agent가 어떤 state에 있는 것이 얼마나 좋은지, 어떤 state에서 어떤 action을 하는 것이 얼마나 좋은지를 표현하기 위해서 기대되는 Return의 크기를 사용하는 것이 합당하다. 따라서 Value function은 Expected Return을 결과값으로 제공하는 함수이다.
다만 Value function이라는 것은 어떤 State에 어떤 Action을 할 것인지에 따라서 달라지기 때문에, Policy라고 부르는 특별한 행동 규칙에 종속적이다. 정책은 $\pi$를 통해서 표현하며, $\pi(a \mid s)$는 State s에서 Action a를 할 확률이 얼마나 되는 지를 정의하는 것이다.
3장의 처음에서 정의한 것처럼 Value function은 State-value function과 Action-value function으로 나눌 수 있으며 모두 특정 policy에 의해 종속적이기 때문에 아래 2가지의 가치함수가 존재한다.
- State Value Function for Policy $\pi$
- Action Value Function for Policy $\pi$
Value Function은 경험을 통해서 추정할 수 있다. 무작위 표본을 통해서 Value Function을 Update하는 Monte-Carlo 방법이나 TD 방법을 통해서 Model을 정확하게 알지 못하는 경우에 대해서도 표본을 통한 Value function 근사를 진행할 수 있다. 또한 State나 Action의 개수나 너무 많아서 현실적으로 모든 경우에 대한 Value function을 작성할 수 없을 경우, 일반적인 인공지능에서 사용하는 instructive feedback을 사용하여 파라미터를 사용한 근사 또한 가능하다.
Value Function의 한가지 근본적인 특성은 Recursive한 관계식을 만족한다는 것이다. 이는 Bellman Equation으로 표현될 수 있는데, 먼저 Bellman Function의 개념부터 정리해보겠다.
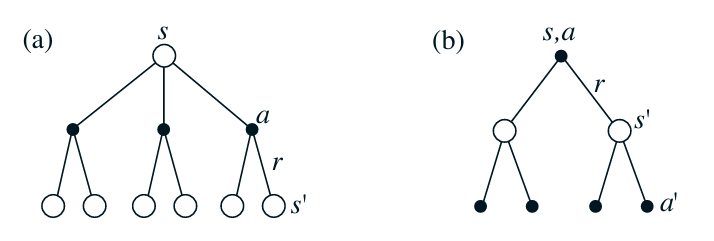
위 상황에서 하얀 동그라미는 State를, 검은 동그라미는 Action을 의미한다. (a) 가정에서는 정책 $\pi$에 따라 하나의 State에서 총 3가지 Action이 가능하고, 각 Action에 따라서 다음 state s’에 도달하는 Backup Diagram을 표현하고 있다. 이는 각각의 action을 취할 확률과 그로 인해 다음 state에 도달할 확률을 고려하여 reward와 다음 state의 가치를 평균한 것이 현재 state의 가치임을 보여준다. 따라서 State Value function은 다음 State로부터 연산할 수 있는 재귀적인 구조를 보인다.
(b)의 가정에서도 (a)와 비슷하게 진행하지만 조금 차이점이 있다. (b)에서는 현재 state에서 수행할 action이 조건부로 주어지기 때문에 reward를 연산하는 과정에서 해당 확률을 작용하지 않는다. 다만, 다음 action value function의 값을 가져오는 과정에서 policy에 따라서 어떤 action을 취할 것인지를 고려해야 한다.
위 내용을 수식을 통해서 정리해보겠다.
먼저 Value Function들 사이의 관계를 생각해 볼 수 있다.
\[\begin{align} v_\pi(s) &\doteq \mathbb{E}_\pi\!\left[ G_t \mid S_t=s \right] \\[4pt] &= \sum_{a\in\mathcal{A}(s)} \mathbb{E}_\pi\!\left[ G_t \mid S_t=s, A_t=a \right]\; \Pr_\pi(A_t=a \mid S_t=s) \\[4pt] &= \sum_{a\in\mathcal{A}(s)} \pi(a\mid s)\; q_\pi(s,a). \end{align}\]위 수식에서 기댓값을 변형하는 관계는 기댓값의 기본 성질을 통해서 도출할 수 있는 관계이다.
\[\begin{align} q_\pi(s,a) &\doteq \mathbb{E}_\pi\!\left[ G_t \mid S_t=s,\; A_t=a \right] \\[6pt] &= \mathbb{E}_\pi\!\left[ R_{t+1} + \gamma G_{t+1} \;\middle|\; S_t=s,\; A_t=a \right] \\[6pt] &= \mathbb{E}\!\left[ R_{t+1} \mid S_t=s,\; A_t=a \right] \;+\; \gamma\,\mathbb{E}_\pi\!\left[ G_{t+1} \mid S_t=s,\; A_t=a \right] \\[10pt] &= \sum_{s'\in\mathcal{S}}\sum_{r\in\mathcal{R}} p(s',r\mid s,a)\, r \;+\; \gamma\, \mathbb{E}\!\left[ \mathbb{E}_\pi\!\left[ G_{t+1} \mid S_{t+1} \right] \;\middle|\; S_t=s,\; A_t=a \right] \\[10pt] &\qquad\text{(tower property / law of total expectation)} \\[10pt] &= \sum_{s'\in\mathcal{S}}\sum_{r\in\mathcal{R}} p(s',r\mid s,a)\, r \;+\; \gamma \sum_{s'\in\mathcal{S}} p(s'\mid s,a)\, v_\pi(s') \\[10pt] &= \sum_{s'\in\mathcal{S}}\sum_{r\in\mathcal{R}} p(s',r\mid s,a)\, \Bigl[r + \gamma v_\pi(s')\Bigr]. \end{align}\]다음 $G_{t+1}$는 기본적으로 현재 t 시점에서 한 시점 뒤로 떨어진 Return을 상정하고 있기 때문에, 이를 반영하기 위해서 전체기댓값의 법칙 (tower property)을 사용하여 전개해야 한다. 위 두 식을 통해서 서로의 관계를 파악했기 때문에 Backup Diagram을 통해서 확인한 것처럼 서로의 다음 state나 state-action에 대한 value로 값을 구해야 한다.
\[\begin{align} v_\pi(s) &= \sum_{a\in\mathcal{A}(s)} \pi(a\mid s)\; q_\pi(s,a) \\[4pt] &= \sum_{a\in\mathcal{A}(s)} \pi(a\mid s) \sum_{s'\in\mathcal{S}}\sum_{r\in\mathcal{R}} p(s',r\mid s,a)\; \Bigl[r + \gamma v_\pi(s')\Bigr]. \end{align}\] \[\begin{align} q_\pi(s,a) &= \sum_{s'\in\mathcal{S}}\sum_{r\in\mathcal{R}} p(s',r\mid s,a)\; \Bigl[r + \gamma v_\pi(s')\Bigr] \\[4pt] &= \sum_{s'\in\mathcal{S}}\sum_{r\in\mathcal{R}} p(s',r\mid s,a)\; \left[r + \gamma \sum_{a'\in\mathcal{A}(s')} \pi(a'\mid s') q_\pi(s',a')\right]. \end{align}\]두 종류의 Value Function 모두 Bellman Equation이 성립하는 것을 수식적으로도 증명할 수 있다.
Bellman expectation equation은 주어진 정책 π에 대해 참값(state-value function 또는 action-value function)이 반드시 만족해야 하는 자기일관성 조건을 나타낸다. 즉, 이 방정식은 value function의 정의로부터 유도되는 고정점 방정식이다. 그러나 실제로는 환경의 전이 확률과 보상 분포를 알지 못하므로, 이 방정식을 직접 계산하여 value function을 구하는 것은 일반적으로 불가능하다.
따라서 value evaluation 과정에서는 다음 상태에서의 정보(보상 및 추정된 value) 를 이용해 현재 상태의 value를 점진적으로 갱신하는 방식이 필요하다. 이러한 갱신 방법의 차이에 따라 Dynamic Programming, Monte Carlo, Temporal-Difference 방법 등이 서로 다른 value evaluation 기법으로 분화된다.
3.5 Grid Space
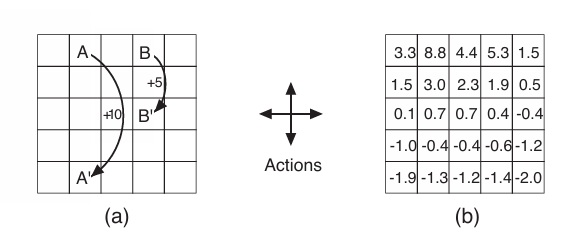
위 그림에서 (a)는 환경의 상태를 보여준다 A의 위치로 가는 경우 위치로 점프하면서 +10의 보상을 받고 B에서도 동일하게 점프하며 +5의 보상을 받는다. 테두리 밖으로 나가는 행동을 했을 경우에는 이전 State와 동일한 자리에 위치하게 되며, -1의 보상을 받게 된다.
이 상황에서 $\pi(a \mid s)$의 값이 전부 $1/4$로 동일한 Policy를 사용한다고 가정했을 때, (b)에서는 value function을 상정하고 있다. 위 상황에서 간단하게 Bellman Equation이 성립함을 확인할 수 있다.
정가운데 0.7은 0.25 x (2.3 + 0.7 + 0.4 -0.4)에서 내림을 진행한 것이고, (3,1)에 위치한 0.1은 0.25 x (-1 + 0.1 + 1.5 + 0.7 - 1)를 진행한 결과이다.
3.6 Optimal Value Functions
RL 문제를 푼다는 것은 가장 많은 보상을 얻는 정책을 파악하는 것과 마찬가지이다. 정책들 중에서 우열을 가리는것은 상당히 모호할 수 있는데, 기본적으로 모든 state나 state-action pair에서 한 정책이 다른 정책보다 좋은 경우만 비교가 가능하다. 이를 수식으로 표현하면 아래와 같다(간단하게 State Value Function만을 고려).
\[\pi \;\ge\; \pi'\;\;\Longleftrightarrow\;\;v_\pi(s) \;\ge\; v_{\pi'}(s),\quad \forall\, s \in \mathcal{S}.\]다수의 Optimal Policy들이 존재할 수 있지만, 이들이 대응되는 Value function은 언제나 동일하다는 점을 기억해야 한다. Optimal Value Function들은 아래와 같이 정리된다.
\[v_*(s) \;\doteq\; \max_{\pi} v_\pi(s), \qquad \forall s \in \mathcal{S}.\] \[q_*(s,a) \;\doteq\; \max_{\pi} q_\pi(s,a), \qquad \forall s \in \mathcal{S},\; a \in \mathcal{A}(s).\] \[q_*(s,a)=\mathbb{E}\!\left[ R_{t+1} + \gamma v_*(S_{t+1}) \;\middle|\; S_t=s,\; A_t=a \right].\]Optimal State Value 값은 행동할 수 있는 것들 중 최상의 가치를 뽑는 것이기 때문에 아래와 같다.
\[\begin{align} v_*(s) &= \max_{a \in \mathcal{A}(s)} q_*(s,a) \\[6pt] &= \max_{a} \mathbb{E}_{\pi_*}\!\left[ G_t \mid S_t=s,\; A_t=a \right] \\[6pt] &= \max_{a} \mathbb{E}\!\left[ \sum_{k=0}^{\infty} \gamma^k R_{t+k+1} \;\middle|\; S_t=s,\; A_t=a \right] \\[6pt] &= \max_{a} \mathbb{E}\!\left[ R_{t+1} + \gamma \sum_{k=0}^{\infty} \gamma^k R_{t+k+2} \;\middle|\; S_t=s,\; A_t=a \right] \\[6pt] &= \max_{a} \mathbb{E}\!\left[ R_{t+1} + \gamma v_*(S_{t+1}) \;\middle|\; S_t=s,\; A_t=a \right] \\[8pt] &= \max_{a \in \mathcal{A}(s)} \sum_{s'\in\mathcal{S}} \sum_{r\in\mathcal{R}} p(s',r\mid s,a)\, \bigl[r + \gamma v_*(s')\bigr]. \end{align}\] \[\begin{align} q_*(s,a) &= \mathbb{E}\!\left[ R_{t+1} + \gamma \max_{a'} q_*(S_{t+1},a') \;\middle|\; S_t=s,\; A_t=a \right] \\[8pt] &= \sum_{s'\in\mathcal{S}} \sum_{r\in\mathcal{R}} p(s',r\mid s,a)\, \left[ r + \gamma \max_{a'} q_*(s',a') \right]. \end{align}\]Optimal Value Function을 구했다면, 이에 맞춰 Optimal Policy를 구하는 것은 아주 간단하다. $V(s)$ 함수를 찾았다면, Greedy하게 다음 Action을 선택하는 것이 Optimal Policy가 되며, $q(s,a)$의 경우는 더 간단하게 최대값을 가지는 action을 선택하는 과정을 거치면 된다.
3.9 Bellman Optimality Equation for Recycling Robot
앞선 예제의 문제를 더 간단히 하기 위해서 State는 h와 l, 행동은 s, w, re로 나타내자. Bellman Optimality Equation을 적용하여 한번 업데이트 하는 예시를 아래와 같이 풀 수 있다.
아래 식은 위에서 정리한 Optimality Equation이다.
\[\begin{align} v_*(s) &\doteq \max_{a\in\mathcal{A}(s)} \mathbb{E}\!\left[ R_{t+1} + \gamma v_*(S_{t+1}) \mid S_t=s,\; A_t=a \right] \\[8pt] &= \max_{a\in\mathcal{A}(s)} \sum_{s'\in\mathcal{S}}\sum_{r\in\mathcal{R}} p(s',r\mid s,a)\, \Bigl[r + \gamma v_*(s')\Bigr]. \end{align}\]State Value Function을 도출해보자. 먼저 High 상태에서는 Search나 Wait의 연산이 가능하고 이때 transition Probability는 아래와 같다.
\[p(h,r_s\mid h,s)=\alpha,\qquad p(l,r_s\mid h,s)=1-\alpha, \qquad p(h,r_w\mid h,w)=1\]위를 바탕으로 Action Value Function은 아래와 같이 정의가 가능하다.
\[\begin{align} q_*(h,s) &= \sum_{s',r} p(s',r\mid h,s)\,[r+\gamma v_*(s')] \\[4pt] &= \alpha\,[r_s+\gamma v_*(h)] + (1-\alpha)\,[r_s+\gamma v_*(l)] \\[4pt] &= r_s+\gamma\bigl[\alpha v_*(h)+(1-\alpha)v_*(l)\bigr]. \end{align}\] \[\begin{align} q_*(h,w) &= \sum_{s',r} p(s',r\mid h,w)\,[r+\gamma v_*(s')] \\[4pt] &= r_w+\gamma v_*(h). \end{align}\]위 과정을 통해서 High state에 대한 Optimality Equation을 아래와 같이 구할 수 있다.
\[v_*(h) = \max\Bigl\{ r_s+\gamma\bigl[\alpha v_*(h)+(1-\alpha)v_*(l)\bigr], \;\; r_w+\gamma v_*(h) \Bigr\}.\]동일한 과정을 Low state에 대해서 구해보면 아래와 같다.
\[v_*(l)=\max\Bigl\{ \beta r_s - 3(1-\beta) + \gamma\bigl[(1-\beta)v_*(h)+\beta v_*(l)\bigr], \;\; r_w+\gamma v_*(l), \;\; \gamma v_*(h) \Bigr\}.\]모델을 정확하게 아는 경우($p(s’,r \mid s,a)$를 알고 있는 경우)라면 직접 Bellman optimality Equation을 반복적으로 적용하여 도달 가능한 최대 value function을 바로 구할 수 있다.
Bellman expectation equation과 Bellman optimality equation의 차이는 다음 상태를 어떻게 “참조하느냐”의 문제가 아니라, 행동 선택을 고정된 정책에 따라 평가하느냐, 아니면 최적화하느냐의 차이에서 기인한다.
Bellman expectation equation은 주어진 정책 π에 따라 행동의 확률적 평균을 취함으로써 정책별 value function을 정의하는 반면, Bellman optimality equation은 각 상태에서 가능한 행동 중 기대값을 최대화하는 행동을 선택함으로써 도달 가능한 최대 value function을 정의한다. 따라서 Expectation을 사용하던지 Maximize를 사용하던지 간에 모두 반복적인 적용은 필수이다.
모델의 알고 있는 DP의 경우 Bellman optimality equation은 Value Iteration의 기반이 되며 Bellman Expectation Equation 은 Policy Iteration의 기반이 된다. 또한 TD의 경우는 두가지가 다르게 반영되어 SARSA나 Q-Learning이 파생되었다.
Bellman Optimality Equation을 Anaytic하게 푸는 것 또한 하나의 방법이다. 다만 이것은 굉장히 특수한 경우이며 모든 가능성을 내다보고 연산하는 Exhaustive Search에 해당한다. 첫번째로 MDP가 성립해야 하고, 두번째로 환경의 모든 것을 알고 있는 FOMDP 가정이어야 한다. 마지막으로 연산이 가능해야 한다. DP와 같이 모델을 전부 알고 있는 경우라도 현실적으로 연산이 불가능한 수준일 경우가 많기 때문에 TD나 MC처럼 점진적으로 온라인으로 근사하는 것이 좋을 경우가 많다.
3.7 Optimality and Approximation
최적 정책을 학습하는 Agent는 이론적인 측면에서는 의미가 있을 수 있지만, 실제로는 일어날 확률이 매우 희박하다. 이는 이론적인 배경을 잘 설명할 수 있으나 실제에 적용한다면 근사값 정도에 그치는 경우가 많다. 완전한 모델이 존재하는 경우 많은 연산량이 필요하고 경험한 내용에 대해서만 Update를 진행하는 경우가 더 효율적인 경우가 많다. 이에 관련해서는 다양한 Policy Evaluation을 다룰 때 더 공부할 수 있을 것이다.