DiLA: Enhancing LLM Tool Learning with Differential Logic Layer

Considering the challenges faced by large language models (LLMs) in logical reasoning and planning, prior efforts have sought to augment LLMs with access to external solvers. Whil…

arxiv.org

소개

이 글은 DiLA(Differential Logic Layer Aided) 방법을 활용하여 대형 언어 모델(LLM)의 논리적 추론 능력을 강화하는 방법을 다룬 연구를 정리한 것입니다. 기존 Chain-of-Thought(CoT) 및 Solver 기반 접근 방식의 한계를 보완하고, LLM이 논리 문제를 보다 정확하고 일관되게 풀 수 있도록 하는 새로운 구조를 제안합니다.

1. LLM과 논리 추론

1.1 Logical Reasoning with LLMs

LLM의 논리 추론은 자연어로 주어진 조건을 기반으로 참/거짓 값을 결정하거나, 제약 조건을 만족하는 해를 찾는 문제를 해결하는 것을 의미합니다.

2. 기존 LLM 추론 방법

2.1 Chain-of-Thought(CoT) Prompting

개념: 복잡한 문제를 풀기 위해 중간 추론 단계를 생성하여 답을 도출하는 방식
장점: 단계별 사고 과정을 명시적으로 표현
한계: 복잡한 문제에서 이전에 생성한 추론 단계를 일관되게 따르지 못하는 경우 발생 (unfaithful reasoning)

2.2 Solver-Aided Approach

아이디어: 외부 논리 솔버를 활용하여 정형화된 논리 문제를 해결
과정:
1. 자연어(NL) 논리 문제를 기호 논리(SAT) 형식으로 변환
2. 외부 솔버를 통해 해 도출
한계: 외부 솔버 호출에 따른 병목 현상, 해가 존재하지 않는 경우 처리 부족

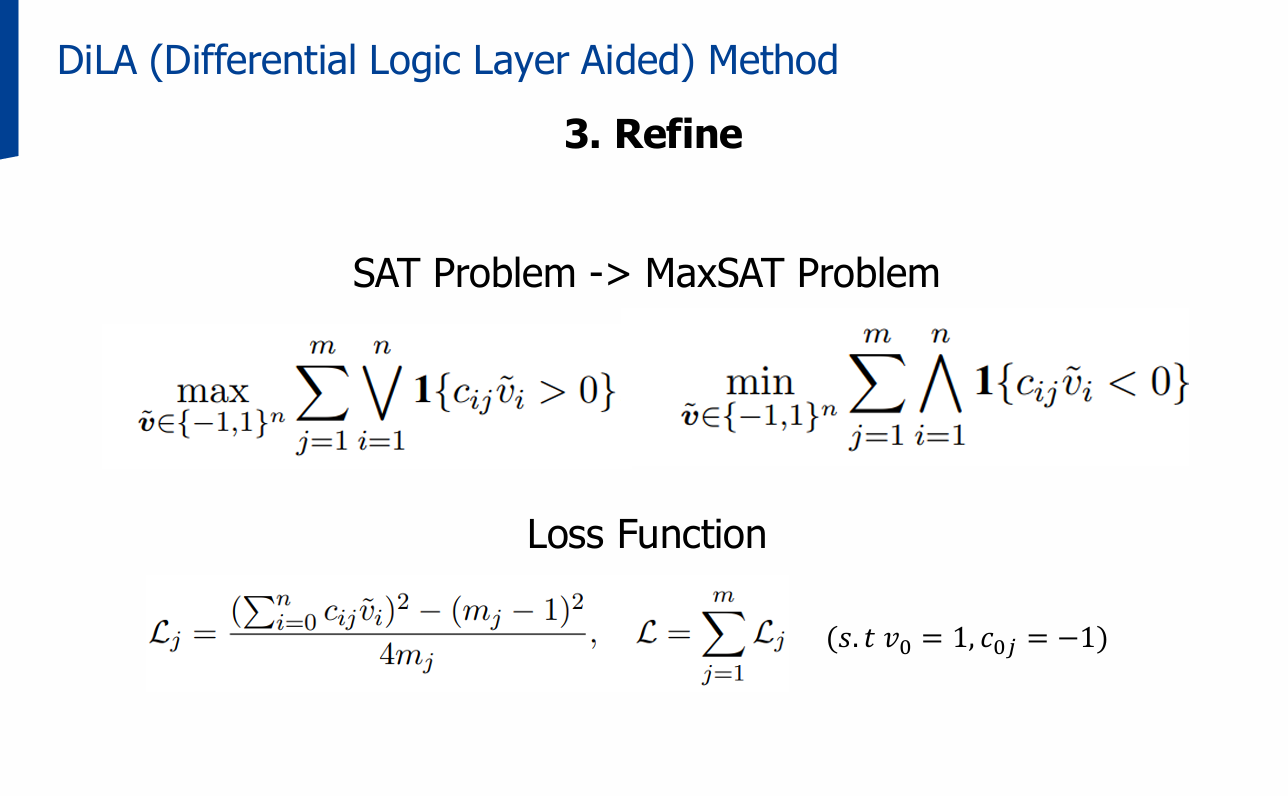
3. DiLA(Differential Logic Layer Aided) 방법

3.1 개요

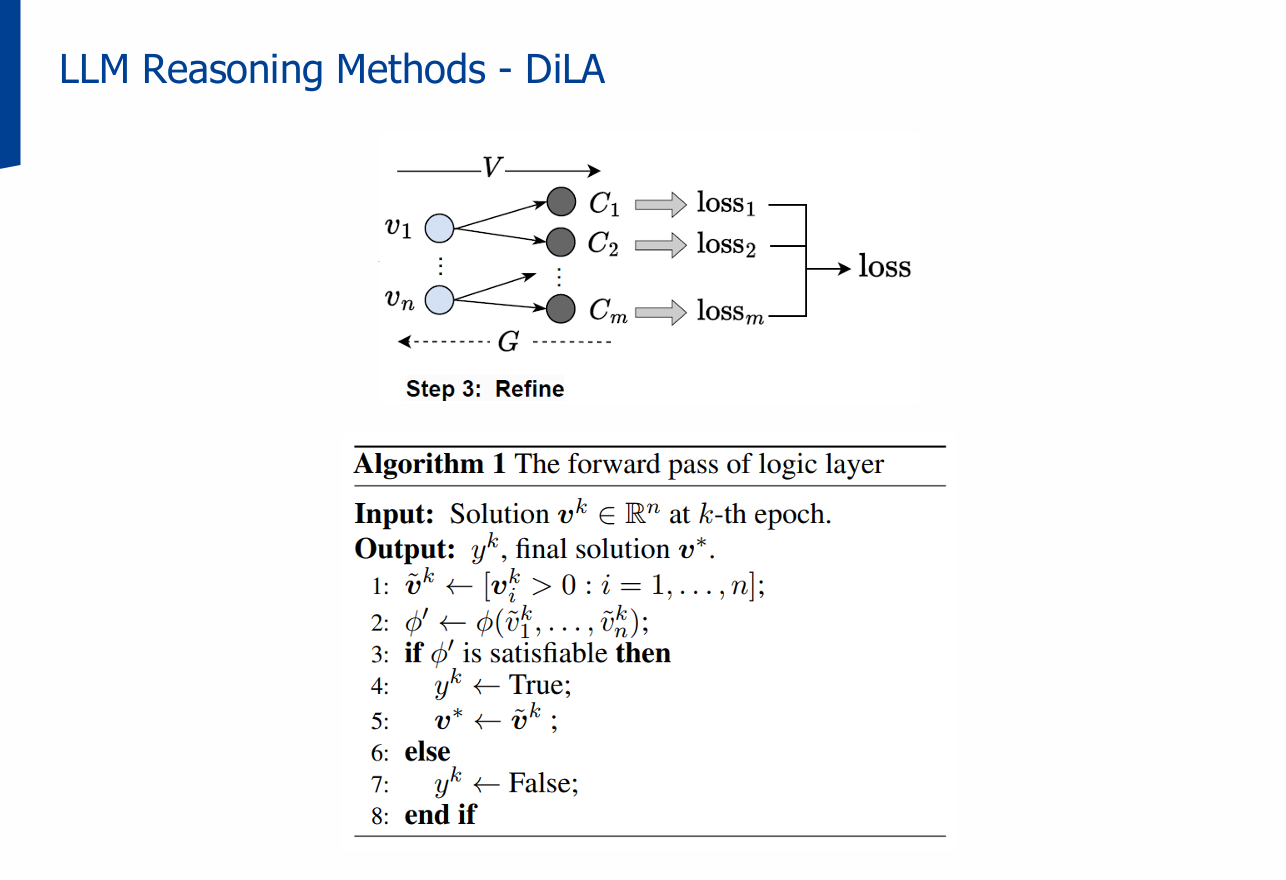
DiLA는 논리 문제를 차분 논리 레이어(Differential Logic Layer)를 통해 네트워크 내에서 직접 해석·최적화합니다.

SAT 문제를 LLM이 이해할 수 있는 자연어와 형식적 제약으로 변환
네트워크에서 순전파/역전파를 반복하며 해를 탐색
특징: 학습 파라미터 없음, 각 절(clause)이 일부 변수에만 연결됨

3.2 절차

1단계: Parse

LLM이 자연어 제약 조건을 SAT 명세로 변환

2단계: Initialize

LLM을 활용해 초기 해를 생성
자연어 질의 예: “주어진 전제에 따라 논리적 해는 무엇인가?”

3단계: Refine

SAT → MaxSAT 변환
최대한 많은 절을 만족시키도록 최적화
손실 함수(Loss Function)를 연속 변수 기반으로 정의하여 미분 가능하게 처리

4. 실험

4.1 실험 과제

Logical Deduction: 객체 순서 유추
Boolean Satisfiability: 모든 제약을 만족하는 변수 할당 찾기
Graph Coloring: 인접한 노드가 같은 색을 가지지 않도록 색칠하기

4.2 결과

비교 대상: 외부 솔버 기반 방법 vs DiLA
DiLA는 해가 존재하는 경우 빠르고 정확하게 결과 도출
그러나 해가 존재하지 않는 경우 처리 부족이라는 한계 존재

5. 결론

DiLA는 LLM의 논리 추론 능력을 강화하는 새로운 접근으로,
외부 솔버의 병목 문제를 줄이고 해를 효율적으로 찾을 수 있음
향후 과제: 해가 존재하지 않는 경우 탐지 강화, 더 복잡한 논리 문제로 확장

발표 자료

자세한 내용은 논문이나 아래 발표 자료로 확인 가능합니다.

Presentation Slides